
2. - SCALAMENTO IN FREQUENZA
Consideriamo la f.d.t. di un filtro passa-basso VCVS del 2° ordine.


Si supponga di volere sintetizzare la f.d.t. passa-basso di Butterworth del 2° ordine:
![]()
Per trovare i valori da assegnare ai vari componenti si devono risolvere le due equazioni
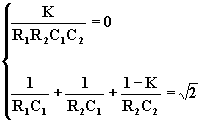
Si hanno cinque variabili (K, R1, R2, C1, C2).
Il sistema è quindi indeterminato poiché si hanno ¥ 3 soluzioni possibili. Occorre quindi assegnare un valore arbitrario a 3 delle variabili.
Una possibile scelta è la seguente:
![]()
Si ha allora:

I polinomi di Butterworth (come anche gli altri) sono normalizzati in frequenza, quindi i valori trovati si riferiscono ad una pulsazione di taglio unitario, cioè di 1 rad/s.
Se si vuole realizzare una f.d.t. con pulsazione w o diversa, si può ottenere la f.d.t. desiderata sostituendo il rapporto s/w o ad s.
Questa operazione di scalamento in frequenza può essere applicata direttamente agli elementi di un filtro attivo RC.
Si supponga di voler sintetizzare un filtro passa-basso di Butterworth con frequenza di taglio di 1KHz.
Passando da ![]() , si
ottiene
, si
ottiene

mentre per la f.d.t. della rete si ha:
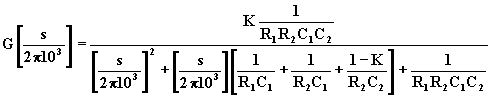
Questa funzione può essere scritta nel seguente modo:
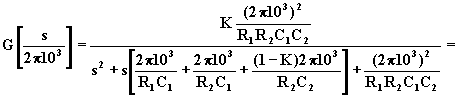
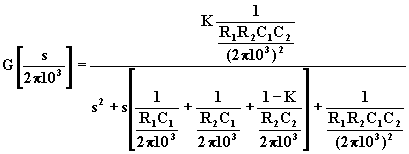
Quindi per realizzare il filtro richiesto, con frequenza di taglio uguale a 103Hz, è sufficiente dividere i valori dei condensatori (o dei resistori) per w o = 2p * 103. Si ottengono i seguenti valori:
![]()
![]() .
.
Si può notare che i valori trovati non sono adatti per una realizzazione pratica del filtro, perché i valori delle due resistenze sono troppo bassi, mentre i valori dei due condensatori sono piuttosto elevati. Si può ovviare a questo inconveniente tenendo conto del fatto che nella f.d.t. della rete le resistenze e i condensatori compaiono sotto forma di prodotti RC. Quindi, se si moltiplicano tutte le resistenze per una certa costante e si dividono tutti i condensatori per la stessa costante la f.d.t. non cambia.
Nel caso in esame si possono moltiplicare tutte le resistenze per 104 e dividere tutte le capacità per 104 e si ottiene:
![]()
Per quanto riguarda K, si ricordi che si ha: ![]() ,
,
K dipende cioè dal rapporto di due resistenze il cui ordine di grandezza è del tutto arbitrario. Dovendo risultare K = 1, ciò può essere ottenuto ponendo RB = 0 e RA =¥ .
Spesso però si preferisce partire da una cella di filtro con frequenza di 1KHz e livello di impedenza di 10KO, e da questa ottenere la frequenza voluta nel seguente modo:
per cambiare frequenza di taglio si moltiplicano tutti i valori dei resistori che determinano la frequenza per il rapporto tra la frequenza fondamentale e la nuova frequenza, o si moltiplicano tutti i condensatori che determinano la frequenza per lo stesso rapporto; non si devono eseguire ambedue le operazioni.
per cambiare il valore di un condensatore in un valore standard, si dividono tutti i valori dei resistori che determinano la frequenza per il rapporto tra il nuovo valore standard e il valore ottenuto dal calcolo.
Le procedure descritte, cio? lo scalamento della frequenza di taglio del filtro e la variazione dei valori dei componenti, sono del tutto generali; un tale procedimento pu? cio?, essere applicato a qualsiasi filtro attivo.