1.6.1. - Risposta con ingresso nullo

supponendo v_i(t) = 0, si ottiene l'equazione omogenea associata:

                                                                                                    (1.6.2)

e l'equazione caratteristica:

                                                                                                                                (1.6.3)

che è, in tale caso, di secondo grado. Per esprimere in forma normalizzata le radici di questa equazione si introducono due parametri, a e w _o, definiti in modo tale che l'equazione (1.6.3) possa essere così scritta:

                                                                                                                                (1.6.4)

Dal confronto tra le equazioni (1.6.3) e (1.6.4) si deducono le espressioni dei parametri a e w _o in funzione degli elementi del circuito; cioè:

                                                                                                          (1.6.5)

dove a e w _o sono numeri reali positivi.

Le soluzioni dell'equazione caratteristica, chiamate anche frequenze naturali del circuito, sono:

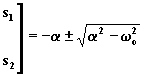                                                                                                                         (1.6.6)

possono essere reali e distinte (se è a > w _o), reali coincidenti (se è a = w _o), complesse coniugate (se è a < w _o). inoltre, si ha:

                                                                                           (1.6.7)

Se le radici dell'equazione caratteristica sono reali e distinte, due possibili soluzioni dell'equazione omogenea sono:

                                                                                             (1.6.8)

pertanto lo è anche una loro combinazione lineare:

                                                                                                                       (1.6.9)

dove K₁ e K₂ sono costanti che dipendono dalle condizioni iniziali.

Se le radici sono reali coincidenti (s₁ = s₂ = -a ), due soluzioni particolari dell'equazione omogenea risultano:

Lo è pertanto anche una loro combinazione lineare:

                                                                                      (1.6.10)

dove K₁ e K₂ sono costanti che dipendono dalle condizioni iniziali.

Se le radici sono reali e distinte si preferisce, in genere, indicare con il risultato dell'estrazione di radice quadrata, potendo scrivere:

                                                                                             (1.6.11)

essendo a _d < a , ambedue le radici sono negative.

Se le radici sono invece complesse coniugate, si pone:

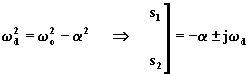                                                                                              (1.6.12)

Sostituendo queste ultime relazioni nell'equazione (1.6.9):

                                                                                                      (1.6.13)

tenendo presente la relazione di Eulero                                                                    (1.6.14)

e raccogliendo a fattore comune e^{-a t}, dall'equazione (1.6.13), si trae:

posto                                                                  (1.6.15)

si ha:                                           (1.6.16)

La costante a , dalla quale dipende in tutti e tre i casi l'andamento decrescente della risposta, viene anche chiamata costante di smorzamento.

Se le radici sono reali e distinte, ambedue risultano negative e l'andamento nel tempo della tensione v_o(t) si ottiene come somma di due esponenziali decrescenti;

Se le radici sono reali coincidenti, si ottiene ancora un valore negativo; pertanto la tensione v_o(t) tende a zero, ma più lentamente perché l'esponenziale viene moltiplicato per una quantità linearmente crescente nel tempo;

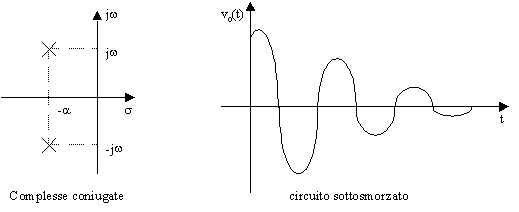
Se le radici sono complesse coniugate, la comune parte reale è negativa; pertanto la tensione v_o(t) ha andamento di tipo sinusoidale, con pulsazione w _d < w _o ed ampiezza tendente esponenzialmente a zero.

Nel primo caso il circuito si dice sovrasmorzato, nel secondo che lo smorzamento è critico e nel terzo che il circuito è sottosmorzato.

Se le radici o la loro parte reale fosse positiva, la risposta risulterebbe esponenzialmente crescente nel tempo, cioè instabilità del circuito.

Poiché le radici dell'equazione caratteristica, ossia le frequenze naturali del circuito, possono essere reali oppure complesse coniugate, è conveniente rappresentarle in un piano complesso, detto piano della frequenza complessa, nel quale l'asse orizzontale rappresenta la parte reale e quello verticale la parte complessa della variabile complessa s. in figura è riportato un esempio di possibile andamento della tensione v_o(t) nei tre diversi casi e la corrispondente posizione delle frequenze naturali nel piano complesso (in ogni caso s₁ + s₂ = -2a ).

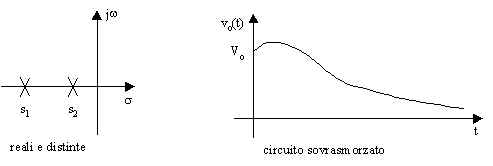
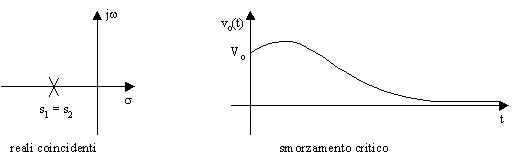
Per poter determinare le costanti che compaiono nelle tre possibili risposte del circuito con ingresso nullo, è necessario imporre le condizioni iniziali, dovute alla presenza di due elementi in grado di immagazzinare en3ergia, l'induttore ed il condensatore. Nel condensatore è la tensione che non può subire discontinuità, mentre nell'induttore lo è la corrente.

Si tiene conto delle condizioni iniziali dando un valore a al tempo t = 0:

Radici reali distinte

Se le radici sono reali distinte, imponendo tali condizioni iniziali nell'equazione (1.6.9); si ha:

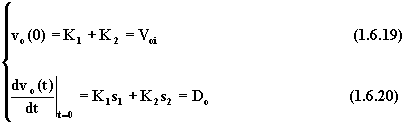
Risolvendo questo sistema di due equazioni, si ricavano K₁ e K₂:

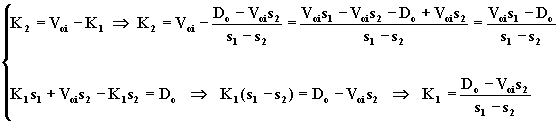
Sostituendo nell'equazione (1.6.9), si ha:

                                                                             (1.6.22)

Radici reali coincidenti

Se le radici sono reali coincidenti, imponendo tali condizioni iniziali nell'equazione (1.6.10); si ha:

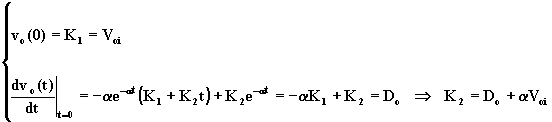
Sostituendo nell'equazione (1.6.10), si ha:

                                                                           (1.6.23)

Radici complesse coniugate

Se le radici sono complesse coniugate conviene sviluppare ulteriormente la (1.6.22). Tenendo presente che è s₁ - s₂ = 2jw _d (equazione (1.6.12)) e che è possibile esprimere in forma esponenziale le radici s₁ e s₂:

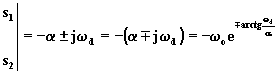                                                                                          (1.6.24)

Dall'equazione (1.6.22) si trae:

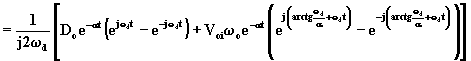
Dalle formule di Eulero

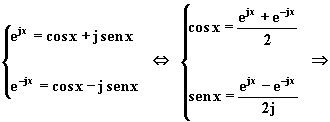
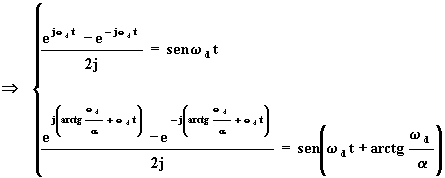
sostituendo, si ottiene:

                                                                 (1.6.25)

La tensione v_o(t) ha pertanto un andamento di tipo sinusoidale con ampiezza decrescente nel tempo perché si è supposta negativa la parte reale delle due radici complesse coniugate.