(3.4.2.1)3.4.2. - Sistemi del secondo rodine
Un sistema si dice del secondo ordine se il denominatore D(s) della f.d.t. è un polinomio di secondo grado in s, che si può esprimere un una delle seguenti forme:
(3.4.2.1)
(3.4.2.2)
(3.4.2.3)
con a , x e Qo
reali e positivi e 
; w
o è detta pulsazione naturale, x è detto
smorzamento, 
è detto fattore di merito,
e a è detta costante di smorzamento. Sono presenti due poli:
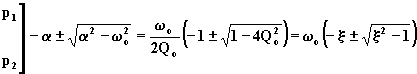(3.4.2.4)
con
.
Per un sistema stabile i poli della f.d.t., dati dalla (3.4.2.4), possono essere:
Reali, distinti e negativi se x > 1, ossia Qo < 0,5;
Reali, coincidenti e negativi se x = 1, ossia Qo = 0,5;
Complessi coniugati con parte reale negativa se x < 1, ossia Qo > 0,5.
In tutti i casi la f.d.t. di un sistema del secondo ordine assume la forma generale:
(3.4.2.5)
Il polinomio N(s) deve essere al più di secondo grado, per un sistema stabile, affinché la G(s) sia convergente per s tendente all'infinito. Il polinomio N(s) assume la forma generale:
(3.4.2.6)
ed a seconda dei valori dei coefficienti a, b e c la f.d.t. può presentare due zeri distinti o coincidenti o complessi; uno zero reale o nessuno zero.
I casi più interessanti di f.d.t. del secondo ordine sono:
Filtro passa-basso, due poli e nessuno zero
(3.4.2.7)
Filtro passa-alto, due poli e due zeri nell'origine
(3.4.2.8)
Filtro passa-banda, due poli e uno zero nell'origine
(3.4.2.9)
Filtro elimina banda, due poli e due zeri immaginari
(3.4.2.10)
Rete correttrice a sella, se p2 > z2 > z1 > p1
(3.4.2.11)
È facile verificare che gli altri casi sono riconducibili ad una combinazione dei precedenti. Ad esempio, se:
,
si può porre nella forma:
,
cioè somma delle f.d.t. di un filtro passa-banda e di un filtro passa-basso.
