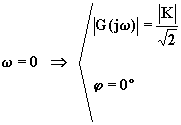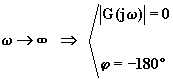; al variare della pulsazione w tale vettore
descrive una curva che prende il nome di diagramma di Nyquist.6.12.2. - Diagrammi di Nyquist
La funzione di trasferimento G(jw ) si
rappresenta, nel piano complesso, mediante un vettore ; al variare della pulsazione w tale vettore
descrive una curva che prende il nome di diagramma di Nyquist.
Ad esempio, la 
si
rappresenta nel piano complesso con una retta avente ascissa costante, pari all'unità;
poiché hanno significato fisico soltanto i valori positivi di w
, il diagramma di Nyquist si riduce ad una semiretta nel primo quadrante.
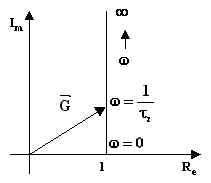
Ad ogni valore di w corrisponde un punto su
tale semiretta; congiungendo uno di tali punti con l'origine degli assi si ottiene il
vettore il cui modulo e il cui argomento
rappresentano il modulo e la fase della f.d.t. alla pulsazione corrispondente al punto
considerato. Per 
il modulo è 1 e
la fase 0°, per 
il modulo diventa
e la fase 
; per 
il modulo
tende anch'esso all'infinito e la fase a 
.
Consideriamo la
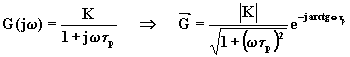
dove
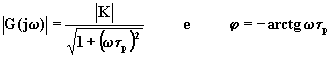
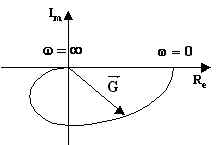
Il diagramma di Nyquist è il seguente:
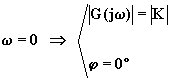
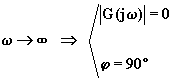
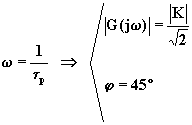
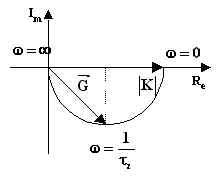
Consideriamo una funzione di trasferimento del secondo ordine con poli reali e negativi
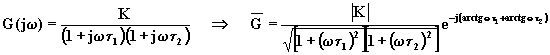
dove
Il diagramma di Nyquist è il seguente:
