Il circuito di un convertitore a scala R-2R a tre bit è quello di figura.

Tale convertitore risolve i problemi relativi al convertitore a resistori pesati; infatti vengono usati due soli valori di resistenza: R e 2R. In questo modo si possono ottenere tutte le resistenze necessarie con variazioni con la temperatura proporzionali fra di loro.

Mentre il convertitore a resistori pesati si basava sul fare contribuire ogni bit con una corrente proporzionale al suo peso, questo convertitore si basa sul diversificare le correnti relative ai vari bit.

Analizziamone il funzionamento, considerando l'ingresso invertente una massa virtuale.

Consideriamo S₀ = 1 e S₁ = S₂ = 0. Attraverso il deviatore elettronico S₀ e la resistenza 2R si avrà una corrente I₀ che arrivata al nodo N (vedi Figura 2) si dividerà in 2 correnti uguali di valore , (infatti le resistenze che vede dal nodo N sono pari a 2R da una parte e 2R dall'altra).

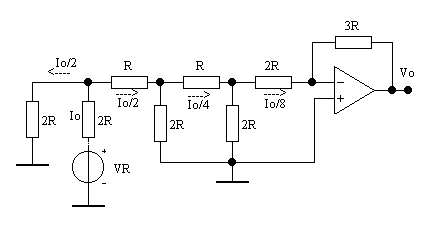
La corrente arrivata al nodo N₁, si dimezza in da una parte e dall'altra. Questa corrente , arrivata al nodo N₂ si dimezza ancora in da una parte e dall'altra. Quindi, S₀ contribuisce con una corrente pari a .

La corrente I_o si calcola riducendo la rete R-2R al seguente circuito:

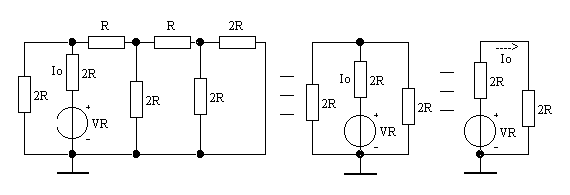
dal quale risulta .

Con S₁ = 1, S₀ = S₂ = 0, si ha:

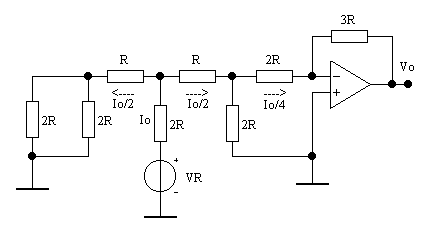
La corrente si divide due volte, per cui S₁ contribuirà con una corrente pari a .

La corrente I_o si calcola riducendo la rete R-2R al seguente circuito:

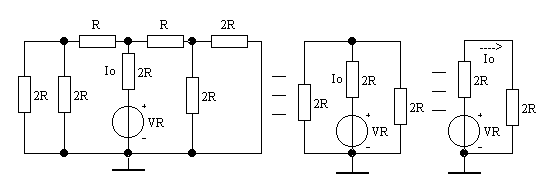
dal quale risulta .

Con S₂ = 1, S₀ = S₁ = 0, si ha:

La corrente si divide due volte, per cui S₂ contribuirà con una corrente pari a .

La corrente I_o si calcola riducendo la rete R-2R al seguente circuito:

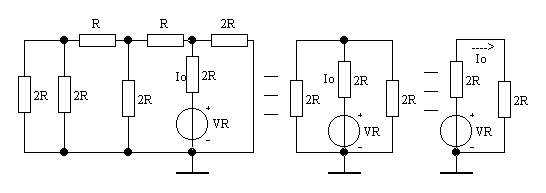
dal quale risulta .

Sovrapponendo gli effetti, si ottiene l'uscita in funzione dello stato dei bit di ingresso:

Più in generale possiamo dire che il bit più significativo (MSB) contribuirà con una corrente pari a , mentre il bit meno significativo (LSB) contribuirà con una corrente pari a .

Un altro modo di ottenere il valore della tensione di uscita V_o, evidenziando la proporzionalità dei contributi di ogni bit dal suo peso, e quello di trasformare il circuito di Figura 1 applicando il Teorema di Thèvenin, nei tre casi illustrati sopra, cioè quando agisce un solo bit per volta. Il circuito derivato è il seguente:

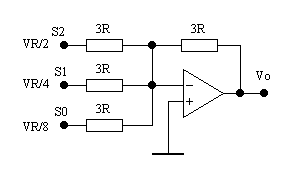
Figura 3

Nel caso di convertitori ad n bit, applicando il teorema di Thèvenin, il bit meno significativo (LSB) contribuirà con una tensione pari a , il bit più significativo (MSB) contribuirà con una tensione pari a .

Il guadagno del circuito (che è un sommatore in configurazione invertente) è unitario, avendo scelto il valore di 3R per la resistenza di retroazione. Se si vuole ottenere un guadagno diverso da 1, basta modificare la resistenza di retroazione. La tensione di uscita, calcolata applicando il principio di sovrapposizione degli effetti, è:

Il V_oLSB, il V_oFS, il V_oMAX saranno:

Generalizzando a N bit, si ha:

Un inconveniente di questo circuito è dovuto agli interruttori S₀, S₁, S₂, ... che sono sottoposti all'intera differenza di potenziale V_R, per cui necessitano di particolari accorgimenti costruttivi e aumentano il costo del circuito integrato. Altro inconveniente è dato dalla variazione delle correnti nelle resistenze, quando si commuta uno degli interruttori (ad es. da 0 ad 1), che producono dei transitori e, quindi, ritardi nella risposta. Per eliminare tali inconvenienti si può utilizzare il convertitore a scala R-2R invertita.