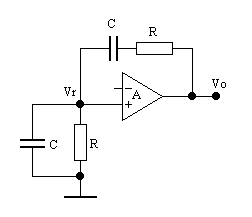
2.1. - Oscillatore a mezzo ponte di Wien
È costituito da un amplificatore non invertente e dea un'opportuna rete di retroazione.

Supponendo che l'amplificatore non assorba corrente all'ingresso, si può aprire la maglia in corrispondenza dei suoi morsetti d'ingresso senza alterare il comportamento del circuito. Se si suppone, poi, nulla anche la resistenza d'uscita, la tensione d'uscita Vo non dipenderà dal carico, e potremo schematizzare l'uscita stessa mediante un generatore ideale dipendente dalla tensione Vi d'ingresso:
![]()
Il circuito equivalente risulterà, allora il seguente:
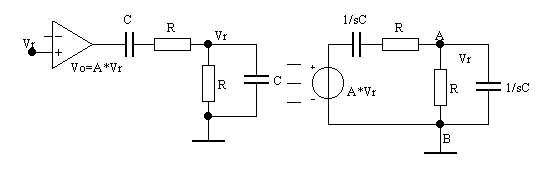
Affinché il generatore ![]() , considerato come un generatore indipendente, determini una
tensione Vr ai capi del parallelo RC si deve ottenere:
, considerato come un generatore indipendente, determini una
tensione Vr ai capi del parallelo RC si deve ottenere:
![]()
Al fine di calcolare VAB, si applica la regola di partizione
sulla serie ![]() :
:
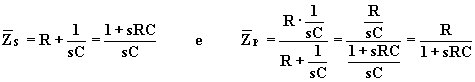
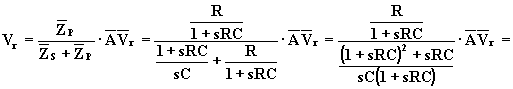

Semplificando Vr in ambo i membri, si ha:
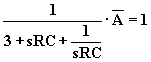
che rappresenta il prodotto ![]() e realizza il criterio di Barkhausen. Posto
e realizza il criterio di Barkhausen. Posto ![]() , si ha:
, si ha:
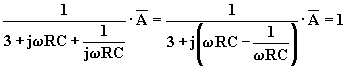
Essendo il secondo membro reale, per essere valida l'uguaglianza, anche il primo membro deve essere reale, ossia b deve risultare reale, e ciò avviene per una sola pulsazione w o:
![]()
In corrispondenza di tale pulsazione, si ha:
![]()
Il sistema può, pertanto, oscillare con pulsazione ![]() purché il guadagno dell'amplificatore
dia positivo e pari a 3. Poiché la rete di retroazione deve attenuare di quanto amplifica
l'amplificatore, affinché sia
purché il guadagno dell'amplificatore
dia positivo e pari a 3. Poiché la rete di retroazione deve attenuare di quanto amplifica
l'amplificatore, affinché sia ![]() , cioè
, cioè ![]() ,
la tensione d'ingresso dell'amplificatore rispetto massa vale 1/3 della tensione d'uscita.
,
la tensione d'ingresso dell'amplificatore rispetto massa vale 1/3 della tensione d'uscita.
Per valutare la stabilità in frequenza, riscriviamo l'espressione di b in funzione del rapporto ![]() . Tenendo conto che
. Tenendo conto che ![]() , si ha:
, si ha:
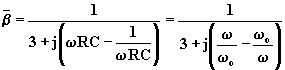
il cui modulo e fase sono:
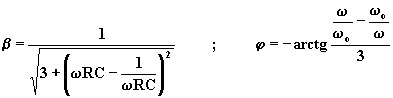
I grafici in funzione di ![]() sono i seguenti:
sono i seguenti:
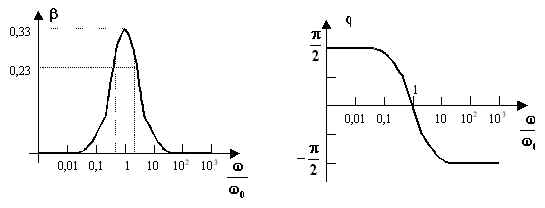
Data la simmetria del grafico di b , possiamo individuare due frequenze di taglio che consentono di definire un coefficiente di selettività nel modo seguente:
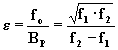 ,
,
dove BP è la banda passante, ed f1 e f2
sono le frequenze alle quali b si riduce di un fattore ![]() e lo sfasamento diventa
e lo sfasamento diventa ![]() .
.
Ricaviamo ![]() e
e ![]() ,
imponendo che a tali valori la tangente di j valga ±1:
,
imponendo che a tali valori la tangente di j valga ±1:
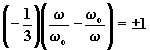
f1 = frequenza di taglio inferiore Þ
![]() Þ tg j = 1 e w = w 1
Þ tg j = 1 e w = w 1
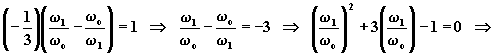
![]()
f2 = frequenza di taglio superiore Þ
![]() Þ tg j = - 1 e w = w 2
Þ tg j = - 1 e w = w 2
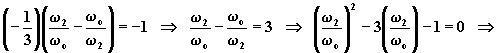
![]()
Sostituendo in e , si ha:
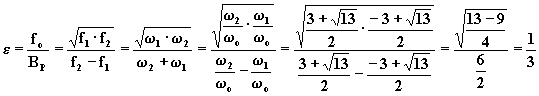 ;
;
valore molto basso, indicante che la rete di retroazione risulta poco
selettiva rispetto alla frequenza. Per valutare la stabilità in frequenza
dell'oscillatore dobbiamo calcolare la derivata prima della fase per la pulsazione ![]() .
.
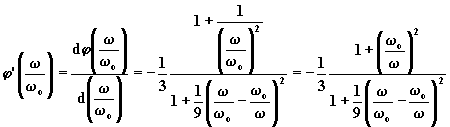
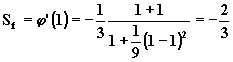
valore basso che indica limitata stabilità in frequenza.