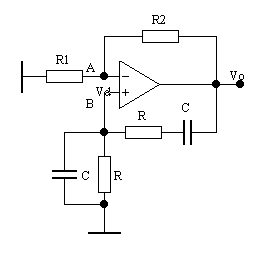
2.2. - Oscillatore a ponte di Wien
L'oscillatore a ponte di Wien deriva dall'oscillatore a mezzo ponte. Si è trasformata la rete di retroazione in un ponte la cui tensione di squilibrio viene applicata ad un amplificatore differenziale.

Supponendo che l'amplificatore non assorba corrente d'ingresso e sia
nulla la sua resistenza d'uscita, possiamo aprire le maglie in corrispondenza dei
terminali d'ingresso, senza alterare il comportamento del circuito, e schematizzare
l'amplificatore mediante un generatore di tensione ideale ![]() . Il circuito equivalente risulta il seguente:
. Il circuito equivalente risulta il seguente:
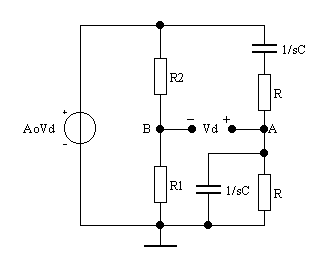
Affinché il generatore ![]() ,
considerato come generatore indipendente, determini una tensione Vd in
ingresso, deve risultare:
,
considerato come generatore indipendente, determini una tensione Vd in
ingresso, deve risultare:
![]()
![]()
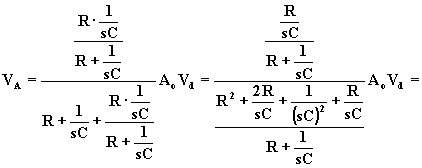
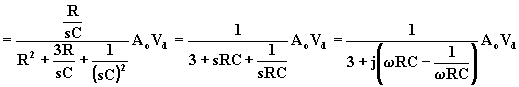
Quindi:
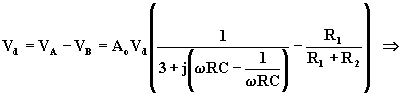
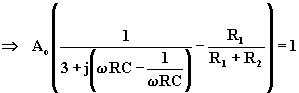
dove
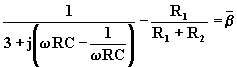
Perché sia ![]() deve risultare nulla, per la pulsazione w
o, la parte immaginaria di
deve risultare nulla, per la pulsazione w
o, la parte immaginaria di ![]() .
.
![]()
A questa pulsazione si ha:
![]()
La condizione a cui devono soddisfare le resistenze R1 e R2 affinché il circuito entri in oscillazione è la seguente:
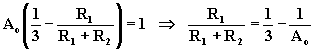
All'aumentare del guadagno Ao dell'amplificatore
differenziale, il potenziale del punto B tende a diventare uguale a quello del punto A,
cioè tende ad equilibrare il ponte (per l'equilibrio occorrerebbe un guadagno
differenziale infinito, ma una tale condizione non è fisicamente realizzabile). È però
conveniente che il guadagno sia più elevato possibile. I valori possibili di Ao
per cui il circuito oscilla sono compresi tra tre e infinito. Esprimendo ![]() in funzione di
in funzione di ![]() , possiamo calcolare il coefficiente di
stabilità in frequenza. Tenendo conto che
, possiamo calcolare il coefficiente di
stabilità in frequenza. Tenendo conto che ![]() , si ha:
, si ha:
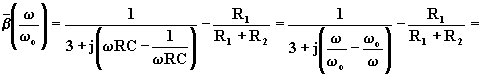
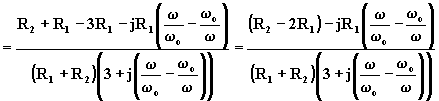
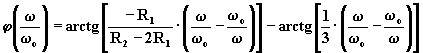
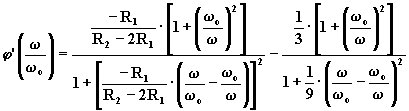
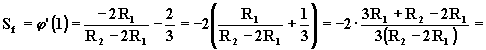
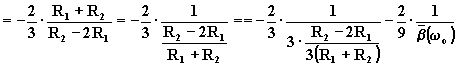
Infatti:
![]()
Per e (selettività) si ottiene:
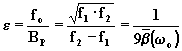 .
.
Poiché il valore di ![]() dipende solo dal valore delle due resistenze R1 e R2, si può
ottenere un qualunque valore per e e Sf. quando
dipende solo dal valore delle due resistenze R1 e R2, si può
ottenere un qualunque valore per e e Sf. quando ![]() si ricade nel caso a mezzo ponte.
si ricade nel caso a mezzo ponte.