Poiché la doppia integrazione di una sinusoide fornisce una sinusoide avente la stessa frequenza, ma sfasata in ritardo di 180°, se si inverte il segnale risultante dalla doppia integrazione si può realizzare uno sfasamento complessivo di 360° e, quindi, riottenere la sinusoide di partenza, purché alla frequenza di oscillazione risulti .

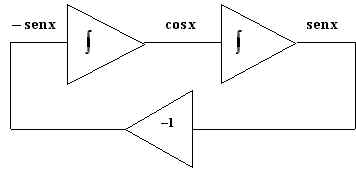
Ricordando che l'integratore nella configurazione non invertente introduce uno sfasamento di 90° in ritardo tra il segnale d'uscita e quello d'ingresso, e che l'integratore invertente introduce uno sfasamento di 90° in anticipotra il segnale alla sua uscita rispetto a quello al suo ingresso, se al posto del secondo integratore si utilizza un integratore invertente, si otterrà uno sfasamento complessivo di zero gradi, rendendo superfluo l'invertitore.

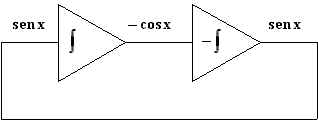
Ponendo, quindi, in cascata ad un integratore non invertente un integratore invertente, si realizza un oscillatore in grado di fornire due uscite sinusoidali sfasate tra lori di 90°, cioè in quadratura, da cui il nome di oscillatore in quadratura.

Il circuito è il seguente.

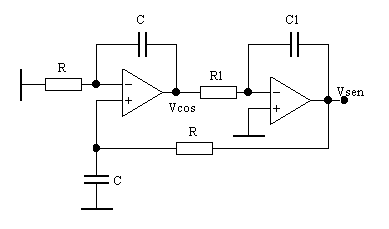
Sempre nell'ipotesi che gli ingressi degli amplificatori non assorbono corrente e che le loro resistenze d'uscita siano nulle, possiamo aprire la maglia all'uscita dell'integratore invertente senza alterare il comportamento del circuito.

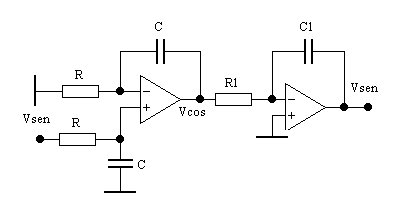
Perché si abbia oscillazione, deve risultare (alla pulsazione w o)

Sostituendo , si ha:

Assumendo che le costanti di tempo siano tutte uguali (cioè imponendo ), si ha:

,

che è la frequenza di oscillazione del circuito. In corrispondenza di tale frequenza il guadagno di entrambi gli integratori risulterà unitario.