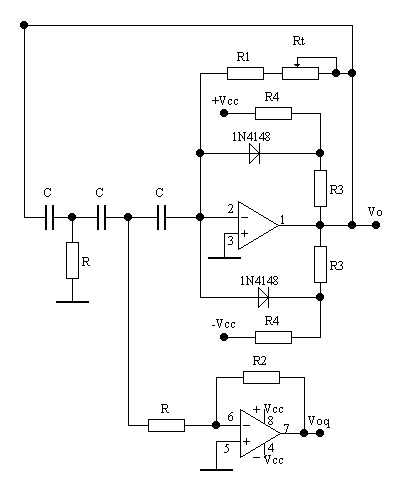
5.2. - Progetto di un oscillatore a rete di sfasamento con frequenza di oscillazione di 1KHz ed uscita
supplementare in quadratura
Si utilizza un'alimentazione duale di ±15V. Anche se questo circuito, una volta innescata l'oscillazione dovrebbe mantenerla senza grosse instabilità e distorsioni, prevediamo l'utilizzo di un limitatore dell'ampiezza per un eventuale controllo dell'amplificazione.
Le modalità di funzionamento del limitatore usato sono riportate in appendice.

Calcolo di R e C
Essendo 1KHz la frequenza di oscillazione, possiamo ricavare la costante di tempo dei gruppi RC:
![]()
Posto ![]() , per R si ha:
, per R si ha: ![]() ,
,
per il quale utilizzeremo il valore commerciale di 10KW . Con tali valori dovremo ottenere una frequenza di oscillazione
![]() .
.
Calcolo di R1 e Rt
Dovendo risultare ![]() ,
poniamo
,
poniamo ![]() .
.
Calcolo del limitatore
Non essendoci grossi problemi perché si stabilizzi l'oscillazione, progettiamo il limitatore perché entri in funzione quando l'uscita supera i 7V. essendo i due rami del limitatore simmetrici, ci limiteremo a calcolarne uno solo, assegnando all'altro gli stessi valori. Assumendo per Vg il valore di 0,7V, si ha:
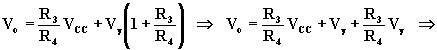
![]()
Posto ![]() per il quale
utilizzeremo il valore commerciale di 4,7KW .
per il quale
utilizzeremo il valore commerciale di 4,7KW .
Calcolo di R2
Volendo un'uscita supplementare in quadratura, dovremo dimensionare R2
in modo che: ![]() per il quale utilizzeremo
il valore commerciale di 68KW .
per il quale utilizzeremo
il valore commerciale di 68KW .
Risultati sperimentali
Regolato il trimmer Rt fino a innescare l'oscillazione,
abbiamo ottenuto su ![]() un segnale
sinusoidale di ampiezza picco-picco di 4,5V, e frequenza 750Hz. La frequenza
risulta inferiore a quella teorica per la capacità C che, date le tolleranze, è
risultata (avendola misurata) di poco più di 12m F.
utilizzando questo valore, per la frequenza si ottiene:
un segnale
sinusoidale di ampiezza picco-picco di 4,5V, e frequenza 750Hz. La frequenza
risulta inferiore a quella teorica per la capacità C che, date le tolleranze, è
risultata (avendola misurata) di poco più di 12m F.
utilizzando questo valore, per la frequenza si ottiene:
![]() .
.
La tensione sull'uscita ![]() ,
come prevedibile, è risultata di 4V picco-picco. Per ottenere la stessa ampiezza
di
,
come prevedibile, è risultata di 4V picco-picco. Per ottenere la stessa ampiezza
di ![]() , aumentiamo la resistenza R2,
ponendole in serie un trimmer di 5KW . Agendo sul trimmer
abbiamo portato l'ampiezza picco-picco di
, aumentiamo la resistenza R2,
ponendole in serie un trimmer di 5KW . Agendo sul trimmer
abbiamo portato l'ampiezza picco-picco di ![]() a 4,5V. A questo punto, per evidenziare la relazione di fase tra
a 4,5V. A questo punto, per evidenziare la relazione di fase tra ![]() e
e ![]() , abbiamo usato le figura di Lissajous, ottenendo un cerchio perfetto, cioè i
due segnali sono risultati perfettamente in quadratura.
, abbiamo usato le figura di Lissajous, ottenendo un cerchio perfetto, cioè i
due segnali sono risultati perfettamente in quadratura.