1.2.2. - relazione intercorrente tra funzione a gradino e funzione impulsiva

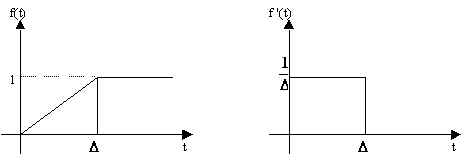
Si consideri la forma d'onda di figura: essa è nulla per t £ 0, linearmente crescente per

0 < t < D ed uguale ad 1 per t ³ D . La derivata di tale funzione è un impulso di area unitaria e durata D .

Facendo tendere D a zero, la f(t) tende alla funzione a gradino unitario u(t) e la sua derivata f '(t) alla funzione impulsiva d (t); si può quindi scrivere:

.

da tale equazione si trae:

.

Infatti, se è t < 0 l'integrale risulta uguale a zero perché non comprende l'impulso di Dirac, che si trova nell'origine degli assi; se invece è t > 0, per ogni t l'integrale è uguale all'unità perché viene integrato l'impulso di Dirac.

Dalla definizione di funzione di Dirac si deduce che, data una generica funzione del tempo f(t), il suo valore nell'istante t = t_o coincide con l'integrale, calcolato tra - ¥ e + ¥ , del prodotto della funzione f(t) e della funzione di Dirac nell'istante considerato:

.

questa è una relazione di notevole importanza nello studio dei segnali campionati.