1.5. - Circuiti del primo ordine

Si definisce circuito del primo ordine un circuito descritto da equazioni differenziali del primo ordine. Ad esempio il quadripolo di figura in cui la relazione esistente tra l'eccitazione v_i(t) e la risposta v_o(t) è la seguente:

                                                                (1.5.1)

dove A e B sono costanti legate agli elementi del circuito.

Per ricavare la risposta di tale circuito bisogna innanzitutto scrivere l'equazione differenziale omogenea associata all'equazione completa, ossia supporre nulla la v_i(t):

                                                                                                                           (1.5.2)

e determinare la funzione complementare, ossia la soluzione di questa equazione.

Poiché tutte le derivate della funzione esponenziale differiscono dalla funzione soltanto per un coefficiente numerico, si può assumere che la variabile dipendente v_o(t) sia del tipo:

                                                                                                                                       (1.5.3)

dove K₁ e K₂ sono costanti che devono essere determinate. Sostituendo nell'equazione (1.5.2) si ottiene:

                                                                      (1.5.4)

Poiché K₁ si deve supporre diverso da zero (K₁ = 0 equivale a supporre v_o(t) = 0), affinché sia verificata questa equazione deve risultare:

                                                                                                                                          (1.5.5)

che è l'equazione caratteristica, la cui soluzione è

                                                                                                                                     (1.5.6)

dove t , avente le dimensioni di un tempo (l'esponente dell'esponenziale deve risultare adimensionale). Viene chiamata costante di tempo del circuito. K₂ ha le dimensioni di una frequenza e viene detta frequenza naturale del circuito. La costante K₂ deve inoltre essere reale e negativa (K₂ positiva fornirebbe una risposta crescente indefinitamente nel tempo).

Per calcolare un integrale particolare dell'equazione differenziale completa è necessario stabilire la forma d'onda del segnale d'ingresso V_i(t) e verificare se un segnale di uguale forma d'onda può essere assunto come integrale particolare. Supponendo di applicare al circuito un segnale costante di ampiezza V_i a partire dall'istante t = 0 (forma d'onda a gradino), si può assumere che, per t > 0 , sia v_o(t) = K₂; sostituendo questo valore di v_o(t) nella equazione (1.5.1) si ottiene:

È verificata pertanto l'ipotesi fatta che una quantità costante possa essere assunta come integrale particolare dell'equazione differenziale completa.

Avendo determinato sia la soluzione dell'equazione differenziale omogenea, sia un integrale particolare, sommandole tra loro si ricava la soluzione dell'equazione differenziale non omogenea (equazione (1.5.1) con v_i(t) = V_i):

                                                                                                    (1.5.9)

La costante K₁ dipende dal valore assunto dalla tensione v_o(t) nell'istante t = 0, ossia nell'istante in cui viene applicato al circuito il segnale d'ingresso.

Si tenga presente che gli elementi reattivi sono elementi che possono immagazzinare energia ed il valore di tale energia dipende dalla tensione ai capi di un condensatore e dalla corrente in una induttanza; indicare la tensione ai capi di un condensatore e la corrente in una induttanza significa specificare l'energia in essi immagazzinata nell'istante considerato .

Supponendo che all'istante t = 0 sia v_o = V_o ed imponendo tale condizione nell'equazione (1.5.9) si ottiene:

                                                                                                 (1.5.10)

Sostituendo questo valore di K₁ nell'equazione (1.5.9), si ricava la relazione finale:

                                                                                       (1.5.11)

ossia la risposta del circuito ad un segnale continuo applicato all'istante t = 0, nell'ipotesi che la tensione iniziale di uscita sia V_o. in figura è riportato l'andamento della tensione v_o(t) per due diversi valori della tensione V_o, uno superiore a V_i/A e l'altro inferiore.

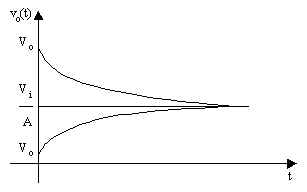
Il primo termine a secondo membro dell'equazione (1.5.11) diminuisce esponenzialmente nel tempo tendendo a zero; esso costituisce un transitorio che, dopo un certo tempo, si esaurisce. Il secondo termine è invece una quantità che rimane inalterata nel tempo e rappresenta quindi la condizione a regime del circuito. In generale la risposta di un generico circuito ad un segnale applicato è costituita da due termini, uno denominato risposta transitoria perché tende esponenzialmente a zero, e l'altro denominato risposta in regime permanente perché rimane invariato nel tempo:

risposta del circuito = risposta transitoria + risposta in regime permanente.

L'equazione (1.5.11) può essere riscritta ne seguente modo:

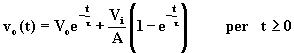                                                                                       (1.5.12)

Il primo termine a secondo membro rappresenta la risposta del circuito nell'ipotesi che sia V_i = 0, ossia che il segnale di ingresso rimanga nullo anche per t > 0; per questo motivo esso viene chiamato risposta con ingresso nullo, oppure risposta libera del circuito. Il secondo termine, invece, coincide con la risposta del circuito al segnale di ingresso nell'ipotesi che sia V_o = 0 e viene chiamato risposta forzata. Poiché si definisce stato di un circuito in un certo istante l'insieme delle condizioni iniziali che determinano in modo univoco, assieme al segnale di ingresso, le correnti e le tensioni in tutti i rami del circuito, il secondo termine a secondo membro dell'equazione (1.5.12) rappresenta anche la risposta del circuito quando esso si trova nello stato zero:

risposta del circuito = risposta con ingresso nullo + risposta nello stato zero.

La risposta con ingresso nullo coincide con la soluzione dell'equazione differenziale omogenea associata all'equazione differenziale completa; quella nello stato zero con la soluzione dell'equazione differenziale completa nell'ipotesi di condizioni iniziali nulle. Per determinare la risposta con ingresso nullo è necessario conoscere lo stato della rete nell'istante iniziale; in questo senso la tensione V_o viene chiamata anche variabile di stato. Per calcolare la risposta nello stato zero bisogna conoscere la forma d'onda del segnale di ingresso.

Tenendo presente che la funzione gradino di ampiezza unitaria è discontinua in t = 0 viene indicata con u(t), l'equazione (1.5.12) può anche essere così scritta:

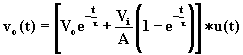                                                                                                        (1.5.13)

utilizzando tale rappresentazione non è necessario specificare che l'equazione è valida per t ³ 0.

Riassumendo, un circuito del primo ordine, descritto da un'equazione differenziale del primo ordine, contiene un solo elemento capace di immagazzinare energia, presenta una sola frequenza naturale ed una unica variabile di stato; inoltre, l'equazione caratteristica associata all'equazione differenziale è di primo grado.