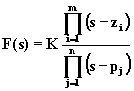2.12. - Antitrasformata di funzioni razionali fratte

Nel caso la F(s) sia una funzione razionale di s, ossia un rapporto di polinomi in s, di tipo proprio (cioè il grado del numeratore è inferiore a quello del denominatore) si può utilizzare il metodo dell'espansione in frazioni parziali per effettuare in modo semplice l'operazione di antitrasformazione. In tale ipotesi, infatti, la funzione F(s) può essere espressa in funzione delle radici dell'equazione che si ottiene uguagliando a zero i polinomi al numeratore ed al denominatore, ossia in funzione dei poli e degli zeri della funzione:

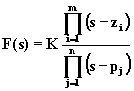                                                                                                                              (2.12.1)

con m<n. Nell'ipotesi che i poli siano tutti distinti tale funzione può essere messa nella forma:

                                                                                 .                                                    (2.12.2)

Se, invece, esistono r poli coincidenti, indicandoli con p_i, risulta:

                                                                    .                                          (2.12.3)

Se esistono anche q radici complesse coniugate semplici, si ha:

                                                .                        (2.12.4)

Per la proprietà lineare della trasformata, ciascuna frazione parziale può essere antitrasformata separatamente; inoltre, l'antitrasformata di ciascuna di esse può essere dedotta direttamente dalle tabelle di antitrasformazione. Si può pertanto ricavare facilmente l'espressione della funzione nel dominio del tempo.

Nel caso di poli reali semplici e poli complessi semplici, per determinare i termini K_j e K_h si utilizzano le seguenti espressioni:

                                                                                                                           (2.12.5)

                                                                                                          (2.12.6)

Nel caso di r poli coincidenti, si può determinare il termine K_1r utilizzando la seguente espressione:

                                                                                                                          (2.12.7)

Gli eventuali rimanenti termini K vengono determinati imponendo l'uguaglianza dei due membri della (2.12.4).