2.4.3. - Derivata nel dominio del tempo

Tra la trasformata di Laplace della derivata di una funzione continua per t > 0 e la trasformata di Laplace della funzione esiste la seguente relazione:

                                                                                                                                          (2.4.3.1)

La trasformata della derivata rispetto al tempo di una funzione è uguale alla differenza tra la trasformata della funzione moltiplicata per la variabile complessa s ed il valore della funzione per t = 0. Qualora la funzione non sia continua per t = o, con f(0) si deve intendere il valore medio tra f(0^-) e f(0⁺).

Dalla definizione di trasformata di Laplace, si ha: .

Integrando per parti, si ha:

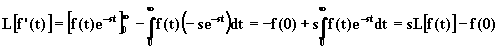
Se la funzione è continua per t > 0 e può essere derivata, utilizzando la relazione precedente, si ha:

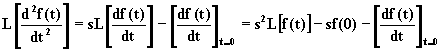                                                          (2.4.3.2)

Più in generale:

                                                                               (2.4.4.3)