3.3.1. - Funzione di rete

Nel dominio della trasformata di Laplace si definisce funzione del sistema, o funzione di rete, il rapporto tra la risposta nello stato zero ed il segnale di ingresso:

                                                                 trasformata di Laplace della risposta nello stato zero

funzione di rete = ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾

                                                                       trasformata di Laplace del segnale di ingresso

In tali condizioni la funzione di rete coincide con la funzione di trasferimento (f.d.t.).

Poiché la trasformata di Laplace della funzione impulsiva d (t) è uguale a uno, la funzione di rete può anche essere definita come risposta del circuito nello stato zero alla funzione impulsiva.

Qualora si voglia calcolare unicamente la funzione di rete si debbono supporre nulli i generatori che tengono conto delle condizioni iniziali relative a ciascun elemento; la rappresentazione degli elementi di circuito risulta pertanto coincidere con quella propria del metodo simbolico. Ne segue che, determinata la funzione di rete, si può dedurre sia la risposta del circuito in regime sinusoidale, ponendo s = jw , sia la risposta nello stato zero ed un segnale qualsiasi, purché L-trasformabile, utilizzando le regole di antitrasformazione.

La funzione di rete di un circuito tempo-invariante è una funzione razionale a coefficienti costanti e può essere, quindi, espressa in funzione delle radici del polinomio P(s) al numeratore e di quello Q(s) al denominatore, ossia dagli zeri z_i e dai poli p_j (dove z_i e p_j possono anche essere complessi):

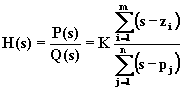                                                                      .                                           (3.2.1.1)

In sostituzione dell'espressione analitica della H(s) si può pertanto fornire la distribuzione dei suoi poli e dei suoi zeri nel piano complesso. Poiché i coefficienti dei polinomi P(s) e Q(s) sono reali, gli zeri e i poli debbono essere reali, oppure complessi coniugati.