4.3. - Diagrammi di Bode
La rappresentazione grafica di modulo e fase della f.d.t. 
al variare di w (o di f) viene di solito effettuata mediante diagrammi
semilogaritmici noti come diagrammi di Bode. Il modulo viene espresso in decibel,
la fase in gradi; la scala delle pulsazioni w (o delle
frequenze f), in entrambi i diagrammi, è logaritmica.
La f.d.t. espressa dalla (4.1.3) può essere riscritta in forma fattorizzata come segue:
,
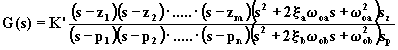(4.3.1)
dove 
;
i termini che rappresentano gli zeri e i poli complessi coniugati sono espressi in forma
di trinomio di secondo grado in cui viene evidenziata la pulsazione propria non
smorzata w o e lo smorzamento x ; sz e sp indicano
rispettivamente gli zeri e i poli nulli. Mettendo in evidenza al numeratore gli zeri reali
non nulli e 
e al
denominatore i poli reali non nulli e 
, si ha:
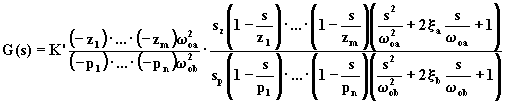
Indicando con K la nuova costante e ponendo 
, si ottiene:
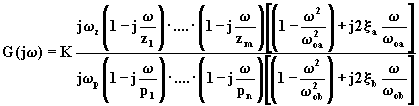(4.3.2)
Supponendo che gli seri 
e i poli 
siano costanti reali negativi negativi o nulli, i relativi valori,
cambiati di segno, rappresentano pulsazioni significative per il funzionamento della rete
e vengono dette pulsazioni critiche:
.
(4.3.3)
L'inverso di ciascuna pulsazione critica è dimensionalmente un tempo ed è detto costante di tempo della rete:
.
(4.3.4)
La (4.3.2) può, quindi, essere scritta nei due seguenti modi:
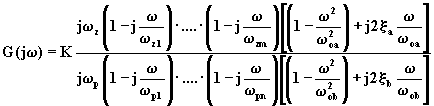(4.3.5)
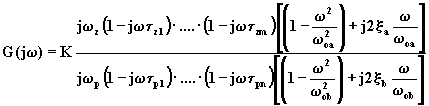(4.3.6)
Numeratore e denominatore della (4.3.6) sono costituiti dal prodotto di più numeri complessi, ciascuno dei quali è funzione della pulsazione w . La risposta in ampiezza è data dal prodotto del valore assoluto della costante K per il modulo di ciascun numero complesso a numeratore, diviso per il modulo di ciascun numero complesso a denominatore:
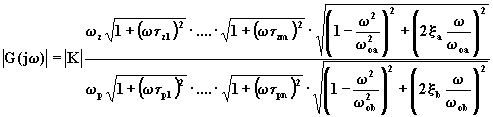(4.3.7)
Se esprimiamo in dB tale risposta in ampiezza, ricordando le proprietà dei logaritmi, si ha:
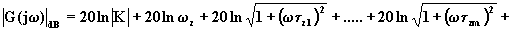
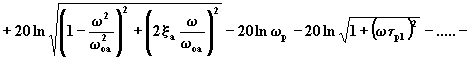
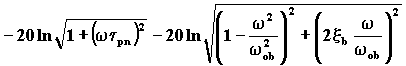(4.3.8)
Tale espressione mostra che la risposta in ampiezza in decibel è rappresentata da una costante sommata algebricamente a diversi termini dello stesso tipo.
Analogamente, per la risposta in fase si ha:
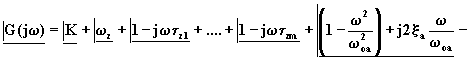
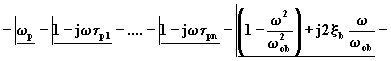(4.3.9)
La risposta in fase complessiva è costituita dalla somma algebrica dello sfasamento relativo alla costante K e degli sfasamenti introdotti dai termini relativi agli zeri e ai poli.
La struttura delle (4.3.8) e (4.3.9) dà la possibilità di costruire i diagrammi di Bode di una rete sommando graficamente i diagrammi relativi alla costante K e a ciascun singolo polo e zero. Noto l'andamento generale del grafico relativo a ciascuno di tali elementi, risulterà molto semplice comporre il diagramma di una qualsiasi funzione di trasferimento con poli e zeri, negativi o nulli.
