4.2. - Risposta in frequenza
Un metodo di indagine particolarmente utile per conoscere il
comportamento dinamico di una rete lineare è quello di studiarne la risposta a regime per
una eccitazione sinusoidale di ampiezza costante al variare della frequenza, ossia la risposta
in frequenza. Il rilievo sperimentale della risposta è di semplice attuazione ed
esistono metodi, ossia i diagrammi di Bode, che consentono di tracciarla
graficamente in modo esauriente, anche se approssimato.
distribuzione
poli e zeri |
diagramma
poli zeri |
G(s) |
caratteristiche
della rete |
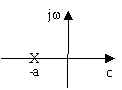
polo negativo
nessuno zero |
|
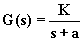
|
filtro passa-basso
del primo ordine
o integratore reale |
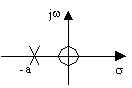
polo negativo
zero nell'origine |
|
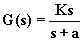
|
filtro passa-alto
del primo ordine
o derivatore reale |
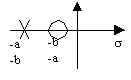
polo negativo
zero non nell'origine |
|
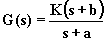
|
rete sfasatrice
o correttrice
del primo ordine |
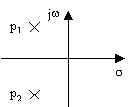
due poli
nessuno zero |
|
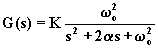
|
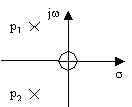
filtro passa-basso
del secondo ordine |
due poli
due zeri nell'origine |
|
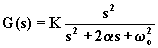
|
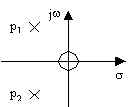
filtro passa-alto
del secondo ordine |
due poli
uno zero nell'origine |
|
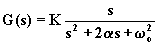
|
filtro passa-banda |
due poli
due zeri immaginari |
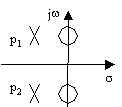
|
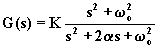
|
filtro elimina banda |
La risposta y(t) di una rete lineare con funzione di trasferimento G(s)
ad un'eccitazione sinusoidale 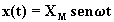 è esprimibile come:
è esprimibile come:
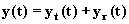 ,
(4.2.1)
,
(4.2.1)
dove yt(t) rappresenta il transitorio, che per
una rete stabile tende ad esaurirsi nel tempo, e yr(t) è la risposta a regime
(0 permanente), di ampiezza costante nel tempo. Utilizzando il metodo della
trasformata di Laplace si riscontra che yt(t) è, in generale, la somma
di funzioni esponenziali decrescenti o di oscillazioni smorzate, legate alla distribuzione
dei poli di G(s) nel piano s = s + jw
, mentre per yr(t) si ricava, invece,
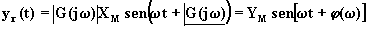 .
(4.2.2)
.
(4.2.2)
La risposta permanente dipende, pertanto, dal modulo e dall'argomento
di G(s) calcolati per s = jw . Più precisamente,
il modulo 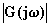 rappresenta il rapporto fra le ampiezze YM e XM dei
segnali sinusoidali, ossia l'ampiezza della risposta e dell'eccitazione. L'argomento
rappresenta il rapporto fra le ampiezze YM e XM dei
segnali sinusoidali, ossia l'ampiezza della risposta e dell'eccitazione. L'argomento 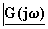 fornisce lo sfasamento
tra risposta ed eccitazione.
fornisce lo sfasamento
tra risposta ed eccitazione.
In conclusione: lo studio della risposta permanente in regime
sinusoidale di una rete può essere condotto direttamente su 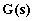 , ponendo
, ponendo 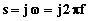 e tracciando i diagrammi del modulo e
della fase al variare di w , o di f.
e tracciando i diagrammi del modulo e
della fase al variare di w , o di f.









