(4.5.3.1)4.5.3. - Zero reale
(4.5.3.1)
(4.5.3.2)
(4.5.3.3)
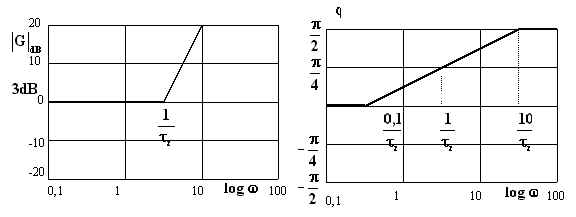
La curva del modulo presenta due asintoti, infatti:
(4.5.3.4)
(4.5.3.5)
All'equazione (4.5.3.4) corrisponde, nel diagramma di Bode per i
moduli, una retta coincidente con l'asse delle ascisse; all'equazione (4.5.3.5) una retta
crescente con pendenza 
passante per il punto 
.
Pertanto il diagramma asintotico di Bode del modulo della funzione espressa mediante
l'equazione (4.5.3.2) è costituita da due spezzate che si incontrano nel punto 
, chiamato anche punto
di rottura, o pulsazione a 3dB, o pulsazione d'angolo.
Il diagramma asintotico del modulo presenta il suo massimo scostamento
dalla curva reale in corrispondenza del punto di rottura; infatti, per 
, ossia per , risulta:
.
Anche per quanto riguarda la fase j si determinano gli asintoti; risulta:
All'equazione (4.5.3.6) corrisponde, nel diagramma di Bode per la fase,
una retta coincidente con l'asse delle ascisse e all'equazione (4.5.3.7) una retta
parallela a tale asse; poiché i due asintoti non hanno alcun punto in comune, è
necessario introdurre un terzo asintoto per poter approssimare la funzione nell'intorno
del punto 
(), punto in cui il diagramma asintotico
e la curva reale coincidono. Supponendo che si possa assumere con sufficiente
approssimazione che sia
si individuano due punti di rottura , 
, che possono essere collegati tra loro mediante una linea retta
passante anche per 
.
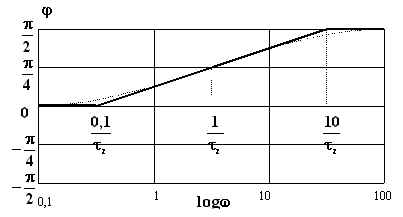
La curva asintotica e quella reale, che coincidono per , presentano il massimo scostamento in
corrispondenza dei punti di rottura; tale scostamento è di circa 6°:
Se lo zero ha molteplicità n: 
(4.5.3.8)
(4.5.2.9)
Per il modulo si ha:
Il diagramma del modulo è ancora costituito da due spezzate: la prima
coincide con l'asse delle ascisse, la seconda interseca tale asse nel punto 
e pendenza 
.
Per la fase si ha:
Per n = 2, si ha:
