6.11. - Interpretazione vettoriale della G(jw )
Le proprietà di una determinata funzione di trasferimento possono
essere dedotte direttamente dal diagramma poli-zeri. Per far questo è necessario tenere
presente che, ponendo ![]() in una generica
funzione G(s), ad ogni valore di w corrisponde quel valore G(jw ) che assume la funzione di trasferimento quando la pulsazione del
segnale di ingresso vale w . Poiché
in una generica
funzione G(s), ad ogni valore di w corrisponde quel valore G(jw ) che assume la funzione di trasferimento quando la pulsazione del
segnale di ingresso vale w . Poiché ![]() individua un punto dell'ordinata positiva del piano complesso s,
ognuno di tali punti rappresenta, pertanto, un possibile punto di funzionamento del
circuito in esame. A ciascuno dei fattori al numeratore e al denominatore dell'equazione
(6.9.1) con
individua un punto dell'ordinata positiva del piano complesso s,
ognuno di tali punti rappresenta, pertanto, un possibile punto di funzionamento del
circuito in esame. A ciascuno dei fattori al numeratore e al denominatore dell'equazione
(6.9.1) con ![]() corrisponde un vettore che
parte dallo zero
corrisponde un vettore che
parte dallo zero ![]() , oppure dal polo
, oppure dal polo ![]() , generico ed è diretto verso il punto jw sull'asse immaginario. Indicando con
, generico ed è diretto verso il punto jw sull'asse immaginario. Indicando con ![]() e
e ![]() il modulo e la
fase del vettore corrispondente allo zero
il modulo e la
fase del vettore corrispondente allo zero ![]() e con
e con ![]() e
e ![]() quelli del vettore corrispondente al polo
quelli del vettore corrispondente al polo ![]() , si può scrivere:
, si può scrivere:
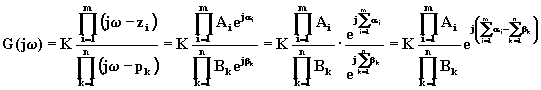 (6.11.1)
(6.11.1)
Pertanto, fissato un certo valore della pulsazione w , il modulo della funzione di trasferimento è proporzionale al rapporto del prodotto delle distanze di ciascuno zero dal punto sull'asse immaginario di valore w e del prodotto delle distanze dallo stesso punto di tutti i poli, la fase della funzione di trasferimento è invece uguale alla differenza tra la somma degli angoli che ciascun vettore relativo ad uno zero forma con l'asse delle ascisse e la somma degli angoli, rispetto allo stesso asse, che forma ciascun vettore relativo ad un polo.