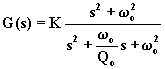6.14.7. - Sistema con due zeri complessi coniugati

La f.d.t. normalizzata è la seguente:

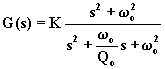                                                                          ,                                         (6.14.7.1)

Posto , si ha:

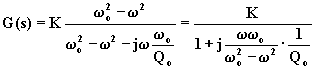                                                       ,                       (6.14.7.2)

al variare di w si deducono le seguenti relazioni:

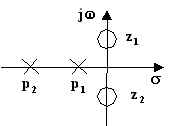
Pertanto un circuito con una f.d.t. di questo tipo presenta una attenuazione infinita in corrispondenza alla pulsazione , e viene, per questo motivo, chiamato filtro elimina-banda. Poiché il valore della f.d.t. sia alle basse frequenze che alle alte frequenze è pari a K, interessa determinare l'intervallo di frequenza in corrispondenza alle quali risulta ; tale intervallo viene anche chiamato banda di reiezione. Risulta:

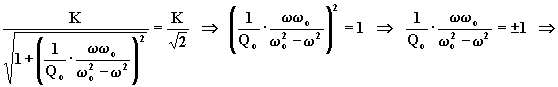
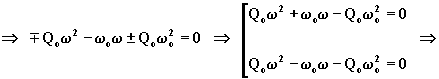
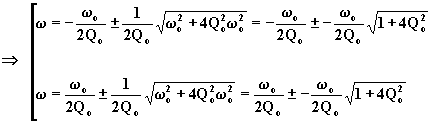
da entrambe si scarta la soluzione col segno meno davanti alla radice, perché inaccettabile una soluzione negativa. Le frequenze sono quindi:

.

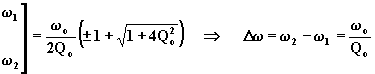Pertanto, anche la banda di reiezione è uguale al doppio del valore assoluto dell'ascissa comune dei due poli.