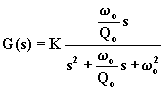,
(6.14.6.1)6.14.6. - Sistema con uno zero nell'origine
La f.d.t. normalizzata è la seguente:
,
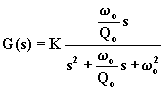(6.14.6.1)
Posto 
, si ha:
,
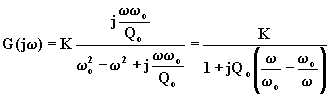(6.14.6.2)
al variare di w si deducono le seguenti relazioni:
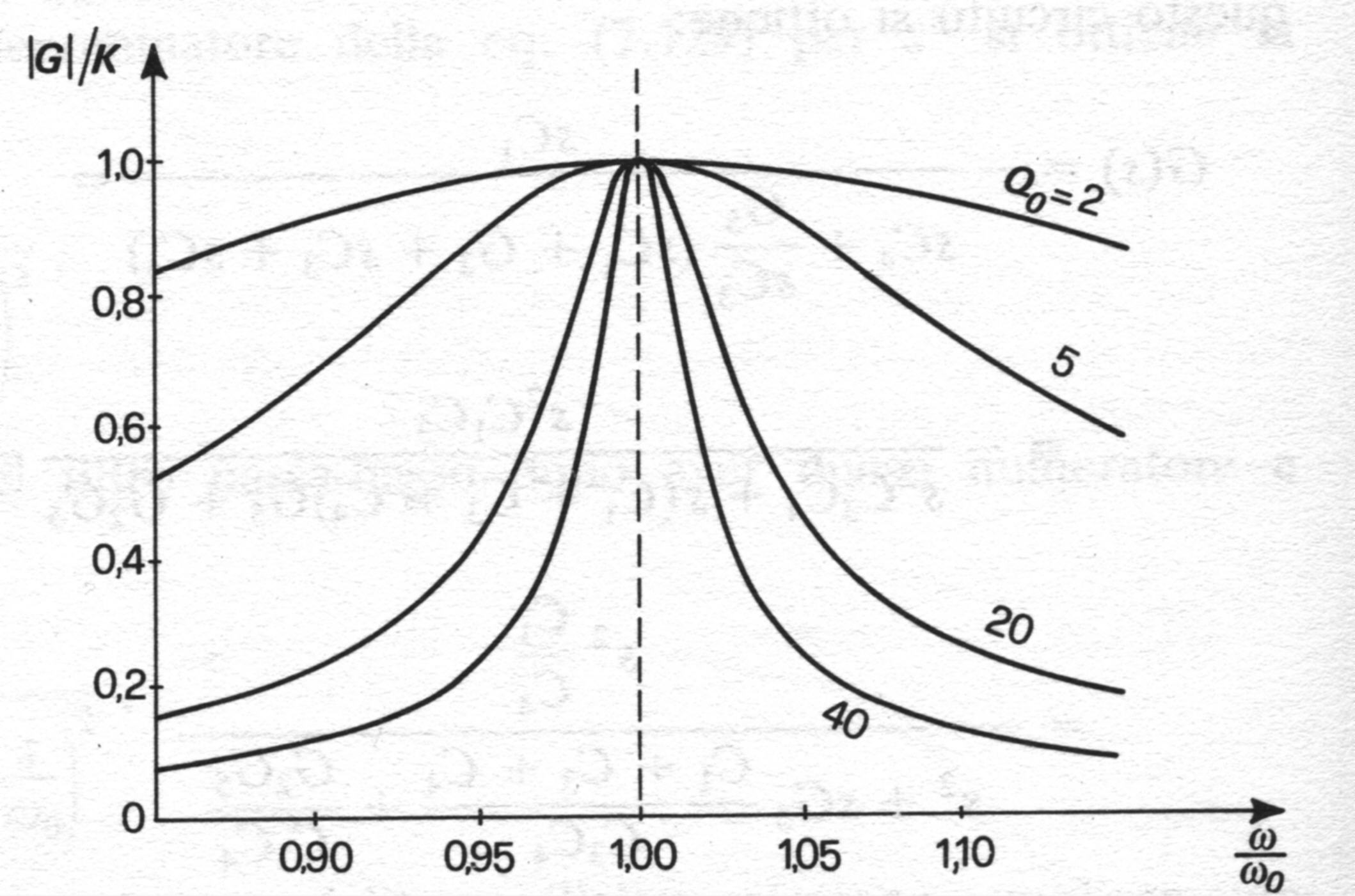
Poiché una rete con una f.d.t. di questo tipo attenua sia alle basse
che alle alte frequenze, esso può essere genericamente chiamato filtro passa-banda.
Per 
la f.d.t. presenta un massimo che
vale K. Per ricavare tale massimo bisogna prima determinare il modulo di 
e imporre che sia nulla la sua derivata
rispetto a w .
,
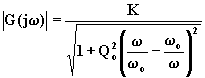(6.14.6.3)
essendo il denominatore sicuramente positivo, e tale anche il termine 
, la diseguaglianza si riduce alla seguente:
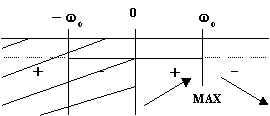
si ha un massimo per 
.
Essendoci tale massimo, interessa determinare la banda passante del
filtro, ossia le pulsazioni in corrispondenza alle quali risulta 
. Segue:
.
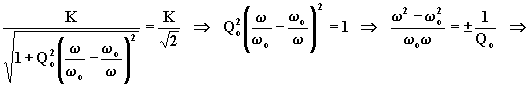
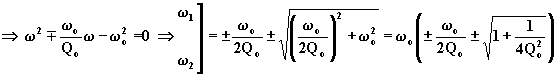Poiché sia 
che 
debbono essere positivi è necessario
escludere la soluzione con ambedue i termini negativi, e quella nella quale la radice
quadrata ha segno negativo perché il valore sotto radice è sicuramente maggiore
dell'unità; segue:
.
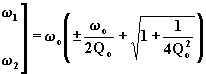Da tale relazione si trae:
;
(6.14.6.4)
Pertanto la banda passante 
, uguale al doppio del valore assoluto dell'ascissa comune dei due poli,
risulta tanto più stretta quanto più è elevato il 
del circuito. Si osservi inoltre che il diagramma del modulo presenta
simmetria geometrica rispetto a 
.
Qualora sia 
,
sviluppando in serie di McLaurin la radice quadrata risultano trascurabili i termini di
grado superiore a 
:
;
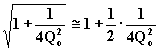pertanto si può scrivere:
.
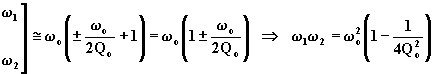In prossimità del massimo il diagramma del modulo presenta simmetria aritmetica; pertanto, qualora la banda sia sufficientemente piccola, si può supporre che essa appartenga alla regione nella quale la simmetria si può supporre di tipo aritmetico.
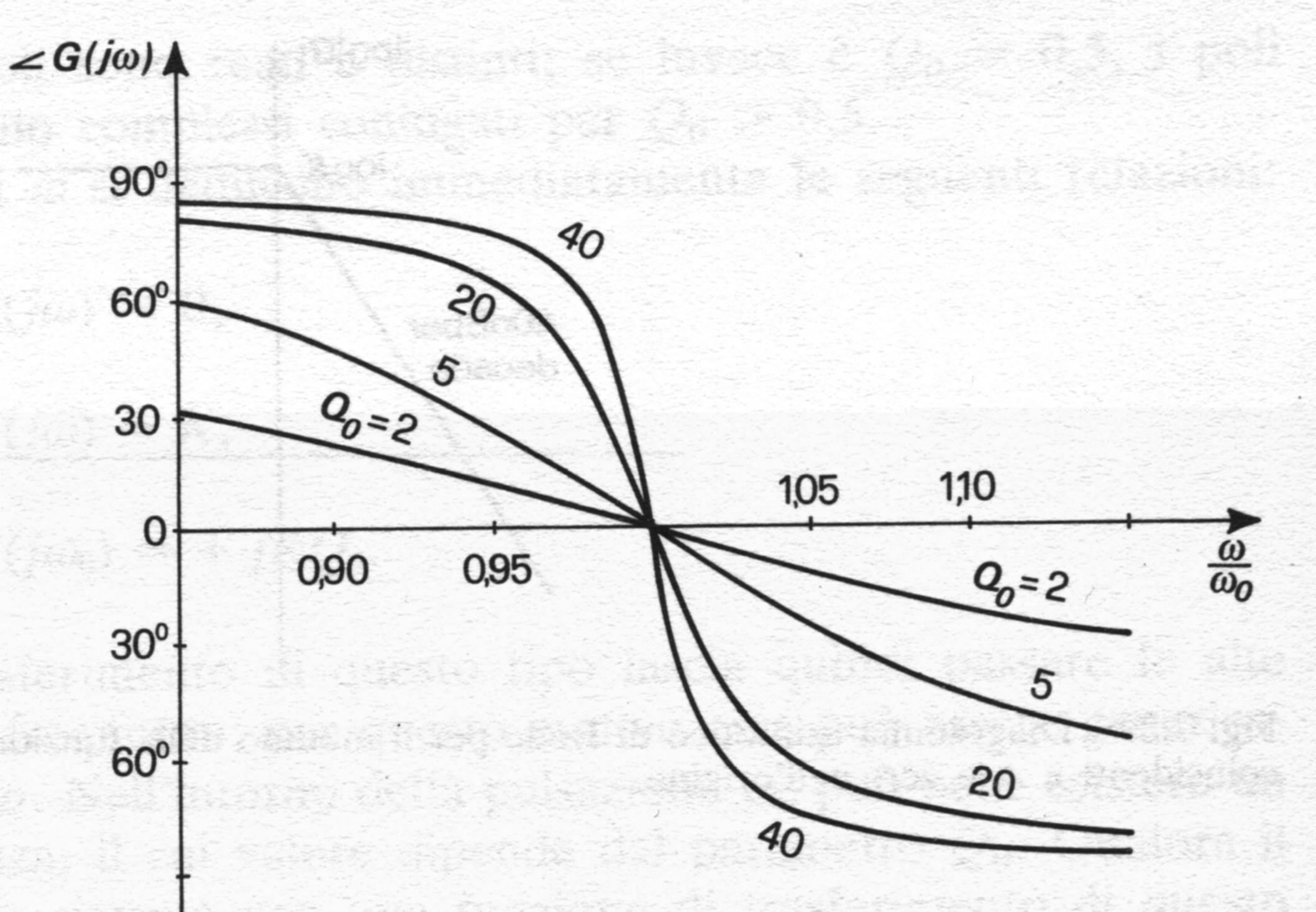
La fase risulta:
,
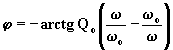(6.14.6.5)
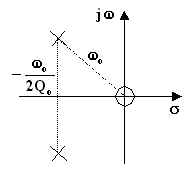
Anche la fase dipende dal valore di .
