6.14.5. - Poli complessi coniugati e poli reali coincidenti

Il modulo della espressa dalla (16.4.4.2) è il seguente:

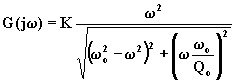                                                                .                                  (6.14.5.1)

Da tale relazione si deduce che:

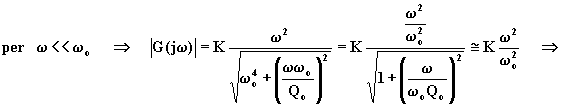
Alla prima relazione corrisponde una retta crescente con pendenza , alla seconda una retta parallela all'asse delle ascisse. I due asintoti si incontrano nel punto , che rappresenta pertanto il punto di rottura.

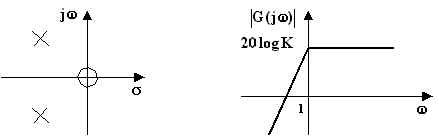
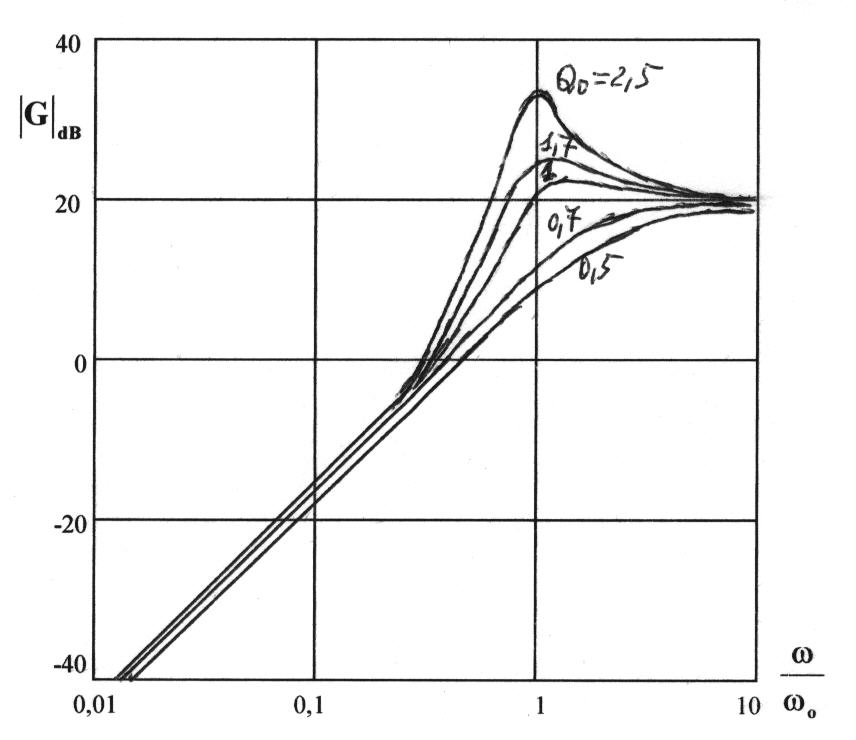
Per in realtà risulta: ; all'aumentare di il diagramma di Bode per i moduli in prossimità di si incurva verso l'alto e presenta un massimo qualora risultino reali le soluzioni dell'equazione . Indicando con la soluzione di questa equazione, si può dimostrare che essa vale:

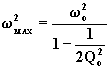                                                                                                                               (6.14.5.2)

Affinché sia reale è necessario che sia . Pertanto, all'aumentare di e per valori di compresi tra e , la curva del diagramma di Bode per il modulo si sposta verso l'alto senza avere un massimo; per la curva presenta un picco per ; tale valore è sicuramente inferiore a e tende a all'aumentare di , ossia all'accentuarsi del picco.

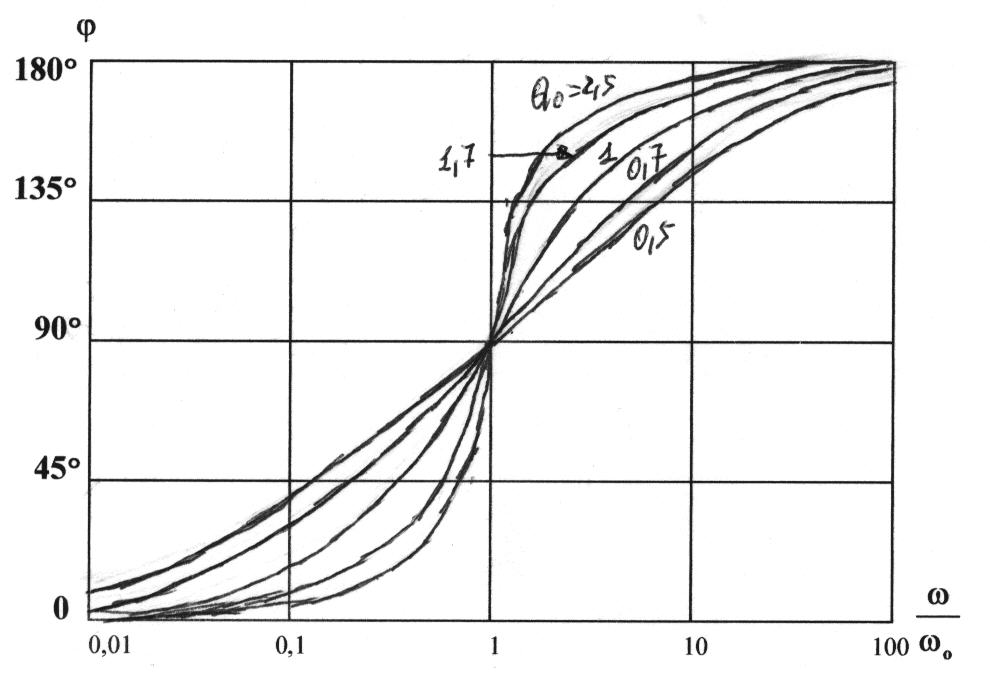
La fase della (6.14.1.2), supposto , risulta:

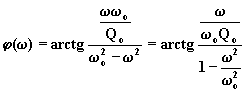                                                                                                 (6.14.5.3)

Anche la fase dipende dal valore di .