6.20. - Espressione della funzione di trasferimento e diagrammi di Bode
Noti i poli e gli zeri, è possibile scrivere l'espressione della f.d.t..
Per la rete di figura c con due poli distinti e due zeri nell'origine, si ha:
dove K viene ricavata da 
(infatti alle alte frequenze 
).
Il diagramma del modulo per il caso di poli reali distinti è riportato in figura e può essere tracciato senza dover passare attraverso i diagrammi elementari.
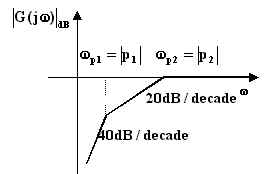
Si tenga presente che, per w crescenti, l'incontro
con un polo produce una variazione della pendenza del diagramma di 
(
se il polo è doppio, 
se è
triplo, ecc.), mentre l'incontro con uno zero causa una variazione di 
(
se lo zero è doppio, 
se è
triplo, ecc.). Pertanto il diagramma inizia con una pendenza di 
per i due zeri nell'origine; la pendenza si
riduce poi a dopo il primo polo e a 
dopo il secondo polo. Poiché si conosce il
valore del modulo alle alte frequenze (
)
conviene, nel disegnare l'andamento, seguire il percorso inverso, cioè partire dalle
frequenze più elevate spostandosi verso le basse.
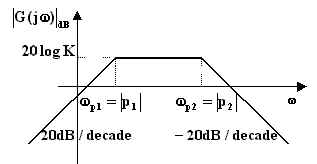
La f.d.t. della rete di figura b, con due poli reali distinti e uno zero nell'origine, è:
Sia per 
che per 
, 
e 
.
Si traccia il grafico partendo dall'origine. Lo zero nell'origine fa
partire il diagramma con pendenza ,
finché il primo polo non lo rende orizzontale. L'incontro col secondo polo porta la
pendenza a 
.
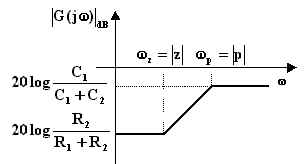
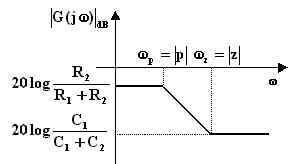
Per la rete di figura a, con un polo e uno zero entrambi negativi, si ha:
dove
Per 
(e quindi 
) la rete diventa un partitore capacitivo, per
cui:
.
Pertanto si ha: 
.
Per 
,
.
In figura sono rappresentati i due diagrammi che corrispondono
rispettivamente ai casi 
e 
.
Per quanto riguarda i diagrammi della fase conviene procedere sommando i contributi dei diagrammi elementari.
