A.4. - Reti simmetriche
Si dice simmetrica una rete che possiede un asse di simmetria.
1. - Una rete simmetrica con eccitazione simmetrica può essere tagliata lungo l'asse di
simmetria.
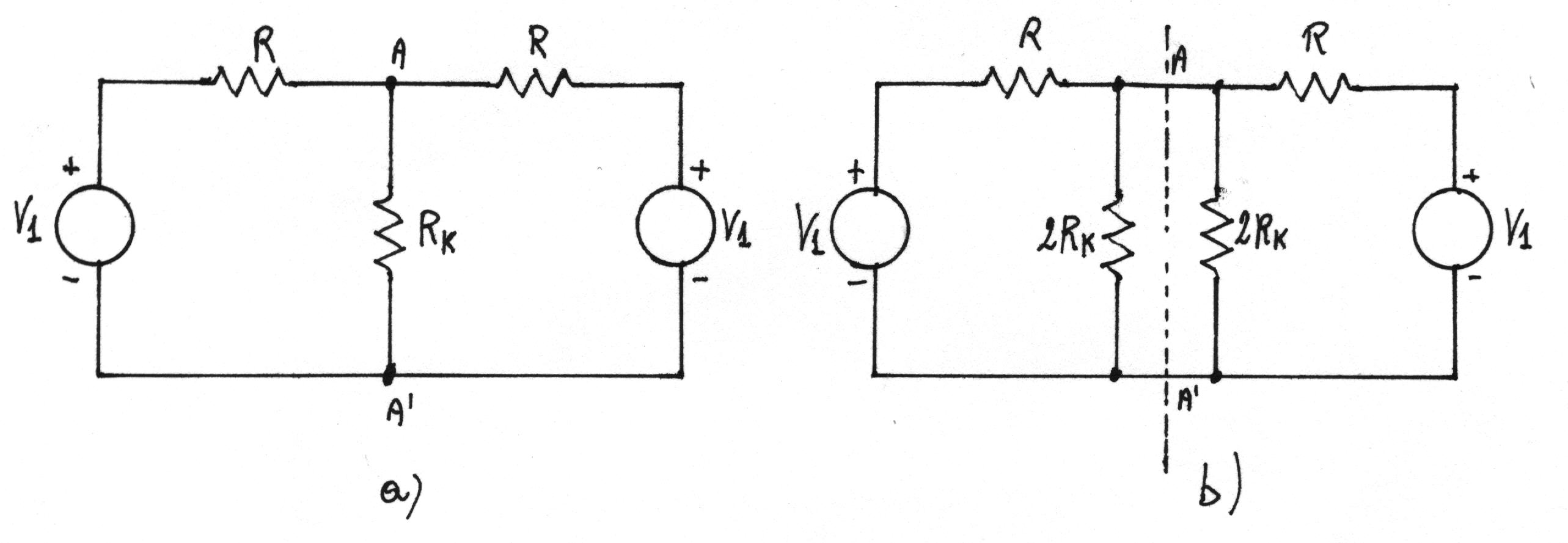
La rete di figura (a) è simmetrica rispetto all'asse verticale AA'. Ciò risulta più evidente in figura (b), nella quale alla resistenza RK si sono sostituite due resistenze in parallelo di valore 2* RK ciascuna.

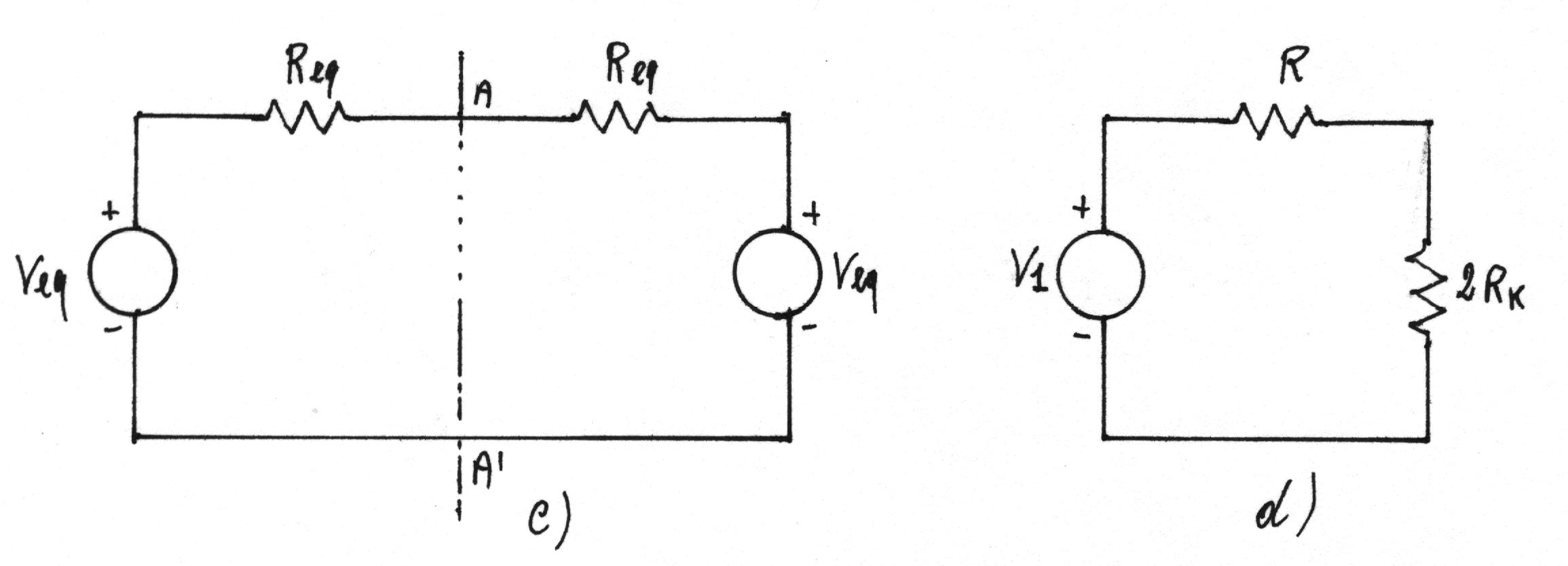
In figura (a) la corrente I che attraversa l'asse di simmetria deve essere nulla. Infatti i circuiti alla destra e alla sinistra dell'asse di simmetria sono due bipoli uguali: se si schematizzano secondo Thèvenin, essi hanno la stessa Veq e la stessa Req (figura (c)). La rete di figura (b) equivale, quindi, alla maglia di figura (c), nella quale non può ovviamente circolare corrente. Se allora è nulla la corrente I che attraversa l'asse di simmetria AA', è possibile separare il circuito alla destra di tale asse in figura (b) da quello alla sinistra, senza perturbare i circuiti stessi. Si può dunque studiare la rete di figura (a) mediante quella di figura (d).
In figura (a) l'eccitazione si dice simmetrica in quanto i due generatori sono identici anche come verso. Se uno dei generatori ha verso opposto rispetto all'altro, la rete è sempre simmetrica, ma presenta eccitazione antisimmetrica.
2. - In una rete simmetrica con eccitazione antisimmetrica i punti sull'asse di simmetria
possono essere cortocircuitati.
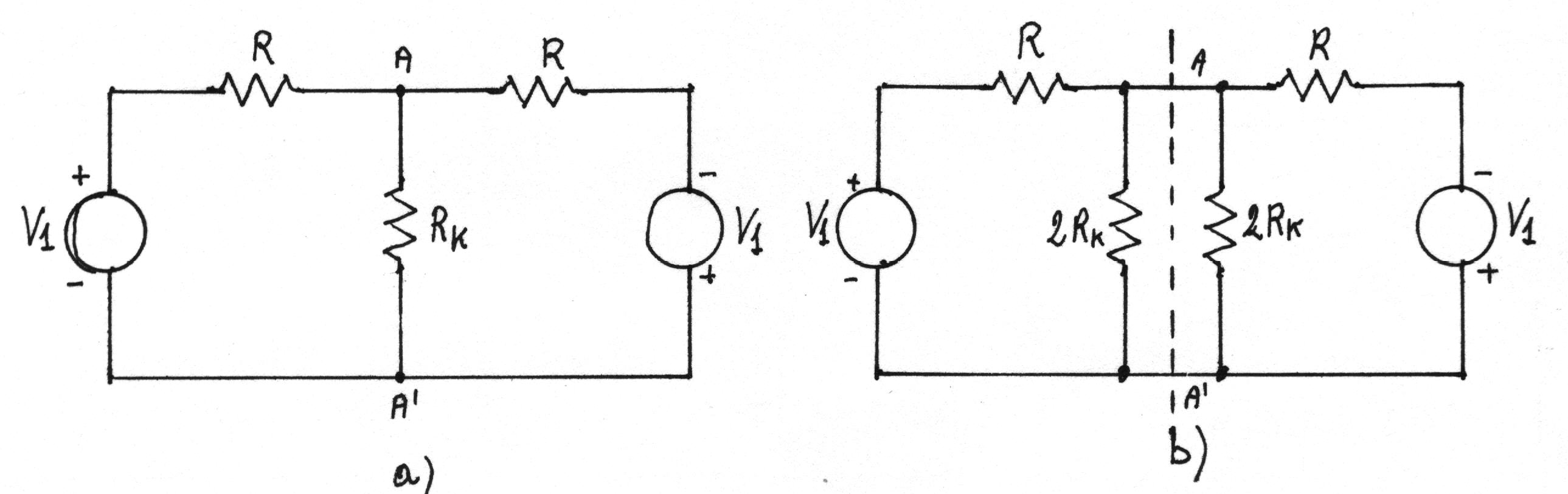
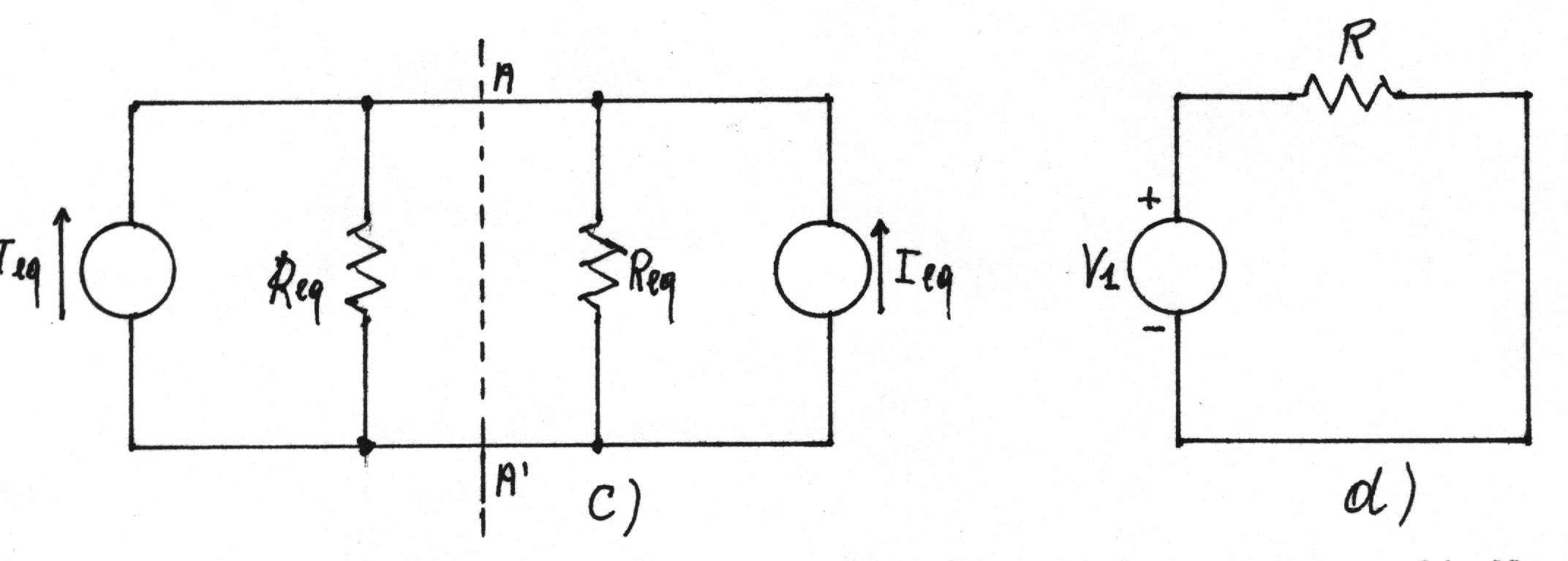
Se alla rete di figura (b) si applica il teorema di Norton, si ottiene il circuito di figura (c), in cui la cadute di tensione sulle Req sono nulle: infatti i due generatori di corrente, pure antisimmetrici, danno luogo in ciascuna Req a due correnti uguali e opposte, come si può facilmente verificare applicando il principio di sovrapposizione degli effetti. I unti A e A' sono quindi allo stesso potenziale: in figura (c), e quindi anche in figura (b), tali punti possono essere cortocircuitati senza perturbare le reti stesse. Si può, dunque, studiare il circuito di figura (a) mediante quello di figura (d).