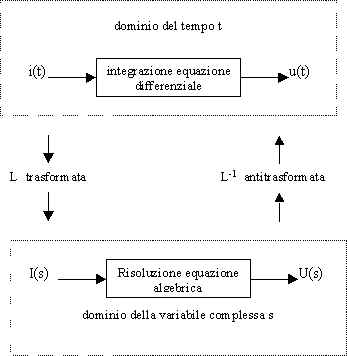
2.1. - Utilità della trasformata di Laplace nella determinazione della risposta di un circuito

Nel determinare la risposta di circuiti contenenti elementi reattivi, tenendo conto delle relazioni tensione-corrente proprie di ciascun elemento circuitale e applicando i teoremi delle reti elettriche, si perviene alla descrizione analitica del circuito mediante equazioni differenziali, la cui soluzione non è spesso semplice. Risulta, allora, vantaggioso utilizzare il cosiddetto metodo simbolico generalizzato, basato sulla trasformata di Laplace.

L'applicazione della L-trasformata ad una funzione del tempo f(t) la trasforma in una funzione nel campo complesso F(s), dove s = s +jw è una variabile complessa.

Questa apparente complicazione comporta un grosso vantaggio: le equazioni differenziali che descrivono il comportamento dei circuiti nel dominio del tempo si trasformano, nel campo complesso, in equazioni algebriche. Inoltre, è possibile, dall'esame della funzione trasformata F(s), risalire all'andamento, almeno qualitativo, della funzione f(t), senza dover necessariamente antitrasformare la funzione.

Si ricava il valore iniziale della f(t) applicando alla F(s) la relazione:

Si ricava il valore finale della f(t), cioè il valore a cui tende f(t) per t ® ¥ , applicando alla F(s) la relazione:

Essendo, normalmente, F(s) il rapporto tra due polinomi, si ricavano le radici del polinomio a denominatore, chiamati poli di F(s), e si tiene presente che ogni polo contribuisce alla f(t) fornendo un termine secondo la seguente tabella. Se i poli sono più di uno, la f(t) risulta la somma dei contributi di ciascun polo.

poli di F(s)			contributo alla f(t)
reale semplice	nullo	s = 0	una costante	K
	negativo	s = p	un esponenziale decrescente
	positivo		un esponenziale crescente
complessi coniugati	parte reale nulla	s = ±jw	una sinusoide
	parte reale negativa	s = s ±jw	una sinusoide con ampiezza decrescente
	parte reale positiva		una sinusoide con ampiezza crescente
reali di molteplicità n	nullo	s = 0	un polinomio di grado n-1
	negativo	s = p	il prodotto di un polinomio di grado n-1 per un esponenziale decrescente
	positivo		il prodotto di un polinomio di grado n-1 per un esponenziale crescente