2.2. - Trasformata di Laplace

La trasformata di Laplace è un'operazione matematica che trasforma una funzione di variabile reale (il tempo t), definita nell'intervallo , in una funzione F(s) della variabile complessa s (, detta pulsazione complessa). Tale operazione consiste nel moltiplicare la funzione f(t) per il fattore e nell'integrare la funzione risultante tra 0 e +¥ ottenendo così una funzione che non dipende più dal tempo, ma solo dalla variabile complessa s:

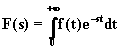                                                                                                                                                      (2.2.1)

poiché la trasformata di Laplace è un operatore che associa ad una funzione f(t) una funzione F(s), si può scrivere simbolicamente:

                                                                                                          ,                                                    (2.2.2)

dove con L si intende la trasformata di Laplace: l'operazione inversa, che permette di passare da F(s) a f(t), viene chiamata antitrasformata di Laplace e viene indicata col simbolo L^-1:

                                                                                                        .                                                  (2.2.3)

L'operazione di trasformazione secondo Laplace è possibile solo se la funzione soddisfa a certe condizioni; può anche accadere che la trasformata esista solo per particolari valori di s. prende il nome di dominio di integrazione o di convergenza l'insieme dei valori della variabile complessa s per i quali risulta definito l'integrale calcolato mediante l'equazione (2.2.1). Per poter effettuare in modo univoco l'operazione di antitrasformazione è ovviamente necessario conoscere non soltanto la funzione F(s), ma anche il suo dominio di convergenza. Tale problema conduce alla formula di Riemann_Fourier

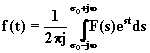
dove s _o è un qualunque valore di ascissa, della variabile complessa s, compreso nel dominio di convergenza.