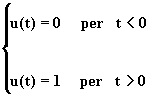
2.3. - Calcolo della trasformata di Laplace di alcune funzioni di uso comune
2.3.1 - Funzione a gradino unitario
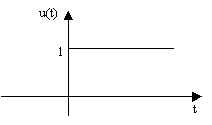
Si definisce gradino unitario u(t) una funzione che soddisfa le seguenti condizioni:
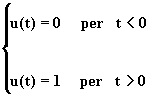
Tenendo presente la definizione di trasformata di Laplace (equazione (2.2.1)), risulta:
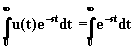(2.3.1.1)
Supponendo che sia s = s , dove s è un numero reale e positivo (s > 0), l'integrando è un esponenziale decrescente e l'aria sottesa da tale curva è finita; infatti si ha:
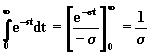
poiché 
per 
. Se, invece, s
fosse un numero reale e negativo (s = -s ), l'integrando
sarebbe un esponenziale crescente e l'aria sottesa dalla curva risulterebbe infinita.
Quindi, per valori reali di s, la trasformata della funzione gradino esiste soltanto se la
s è reale e positiva. Se s è un numero complesso (
), utilizzando le formule di Eulero, si
ha:
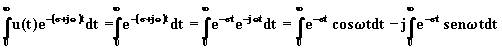
Anche in questo caso, se s > 0 ciascun integrando è una sinusoide di ampiezza decrescente in modo esponenziale; poiché a ciascuno degli integrali dell'equazione (2.3.1.2) corrisponde un valore definito, si può concludere che la trasformata di Laplace della funzione gradino esiste purché la parte reale della variabile complessa s sia maggiore di zero. Calcolando l'integrale, si ha:
.
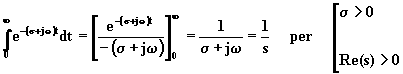
(2.3.1.3)
Anche se la trasformata di Laplace della funzione gradino è definita unicamente per Re(s) > 0, questa condizione deve essere tenuta presente solo quando si effettua l'operazione di antitrasformata al fine di ricavare in modo univoco la funzione di partenza u(t) da quella F(s); in ogni altro caso la funzione F(s) può essere considerata una funzione di variabile complessa definita per ogni valore di s, ad eccezione dell'origine dove assume valore infinito. Essa viene pertanto rappresentata, nel piano della variabile complessa s, con un polo nell'origine.
La funzione gradino è una funzione ideale che presenta una discontinuità per t = 0. Nello studio delle reti elettriche, la risposta ad un gradino di tensione applicato in ingresso fornisce importanti informazioni sul modo e sulla rapidità di risposta della rete.
