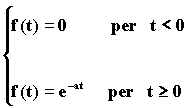
2.3.2. - Funzione esponenziale
La funzione esponenziale è così definita:
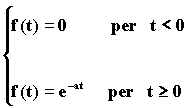

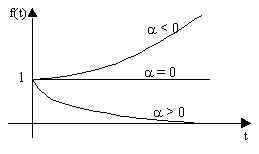
dove a può essere un numero reale o un numero complesso. Se a è un numero reale, f(t) è una funzione reale della variabile reale t; se invece a è un numero complesso, f(t) diventa una funzione complessa della variabile reale t. Una funzione reale di una variabile reale si rappresenta nel piano; una funzione complessa di una variabile reale si rappresenta nello spazio, riportando su un asse il valore di t e sugli altri due la parte reale e la parte immaginaria di f(t). dalla definizione di trasformata di Laplace, si trae:
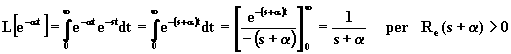
La trasformata di Laplace della funzione esponenziale è una funzione definita solo se è verificata la condizione Re(s+a ) > 0. Qualora, però, non interessi l'operazione di antitrasformata, la funzione F(s) può essere considerata definita per ogni valore di s, eccetto quello per il quale risulta s = a ; nel piano complesso la funzione F(s) presenta un polo per s = -a .
In generale si può dimostrare che:
![]()
In particolare, si ottiene la trasformata di tn se si pone a = 0. Ad esempio, si ha:
Rampa unitaria: n = 1 e a = 0
![]() (2.3.3.2)
(2.3.3.2)
Parabola unitaria: n = 2 e a = 0
![]() (2.3.3.3)
(2.3.3.3)
Cubica unitaria: n = 3 e a = 0
![]() (2.3.3.3)
(2.3.3.3)
In generale: n e a = 0
![]() (2.3.3.3)
(2.3.3.3)