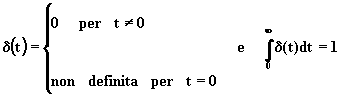
2.3.3. - Funzione impulsiva

La funzione impulsiva è così definita:

           .                            

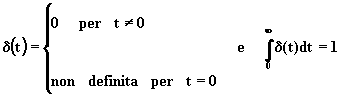
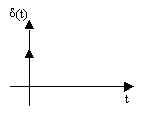
Da tale definizione, si deduce immediatamente l'espressione della sua trasformata di Laplace:

                                                                                   .                                   (2.3.3.1)

Essendo la funzione impulsiva nulla per , si deve considerare l'integrando solo per , dove l'esponenziale è uguale all'unità. La trasformata di Laplace della funzione impulsiva esiste qualsiasi sia il valore della variabile complessa ed è quindi definita per ogni s. È inoltre importante ricordare che la trasformata di Laplace della funzione impulsiva è uguale all'unità.