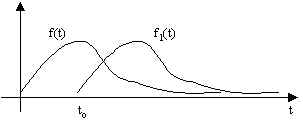
2.4.7. - Teorema del ritardo

Sia F(s) la trasformata di Laplace di una funzione f(t) e f₁(t) una funzione che ha lo stesso andamento della f(t), ma con un ritardo t_o. Dalla figura, nella quale sono rappresentate due funzioni che soddisfano a questa condizione, si deducono immediatamente le seguenti relazioni

Si vuole determinare la trasformata di Laplace della f₁(t). Poiché risulta:

,

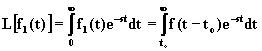posto x = t - t_o, si ha:

;

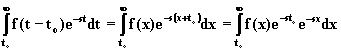infatti è dt = dx e, per t = t_o, risulta x = 0. Applicando la definizione di trasformata di Laplace alla funzione di variabile reale x, si deduce la relazione finale:

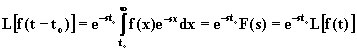                                                                   (2.4.7.1)

La trasformata della funzione ritardata e pertanto uguale alla trasformata della funzione originaria moltiplicata per la quantità .

Ad esempio, la trasformata di Laplace del gradino ritardato vale

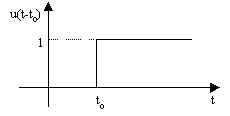
La funzione impulso rettangolare di ampiezza unitaria di figura può essere ottenuta come differenza tre la funzione gradino e la funzione gradino ritardato di un intervallo t_o:

Per la proprietà di linearità la trasformata secondo Laplace di tale funzione vale:

                                        (2.4.7.2)

Si è così ricavata la trasformata di Laplace di un impulso rettangolare di ampiezza unitaria posto nell'origine.