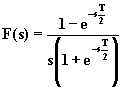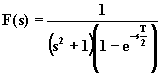2.5. - Trasformata di Laplace di funzioni periodiche

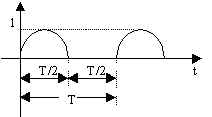
Sia f(t) una funzione definita per t ³ 0 e periodica di periodo T, cioè

Se la funzione f(t) è L-trasformabile su un intervallo di lunghezza T, indicando con F(s) la sua trasformata relativa ad un periodo, si ha:

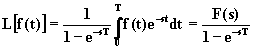                                                               .                              (2.5.1)

Scritto l'integrale di Laplace come somma degli integrali su ciascuno dei periodi:

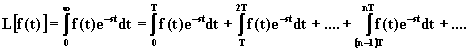                                  ,    (2.5.2)

si effettua il seguente cambiamento di variabile:

I nuovi estremi di integrazione sono 0 e T, per ciascun integrale.

Poiché , la relazione (2.5.2) si riscrive nel seguente modo:

,

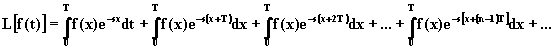che si può anche scrivere:

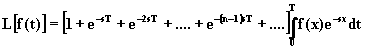                                                .                   (2.5.3)

La serie entro parentesi quadre nella (2.5.3) è una serie geometrica convergente (perché ), la cui somma vale ; l'integrale rappresenta la trasformata di Laplace della f(t) considerata solo nel primo periodo. Pertanto:

.

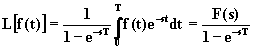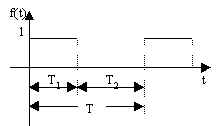
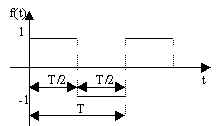
La (2.5.1) permette di determinare la trasformata di Laplace di molte funzioni periodiche di interesse elettronico. Nelle successive figure sono riportate alcune di tali funzioni con le relative trasformate.