2.6. - Funzioni elementari

Per poter calcolare la trasformata di Laplace di una funzione f(t) è necessario che tale funzione sia definita a partire dall'istante t = 0; conviene pertanto assumere che sia .

Ad eccezione della trasformata di Laplace di una funzione ritardata, le funzioni elementari F(s) ricavate precedentemente sono tutte esprimibili come rapporti tra polinomi nella variabile complessa s. In tale caso esse possono essere individuate, a meno di una costante, per mezzo delle radici del polinomio a numeratore e di quello al denominatore, chiamate rispettivamente zeri e poli, e rappresentate per mezzo del diagramma poli-zeri.

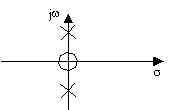
Nella tabella seguente viene fornito un elenco delle trasformate di Laplace di alcune funzioni elementari e, quando possibile, viene fornito il diagramma poli-zeri della trasformata. Si osservi che, dal tipo di diagramma poli-zeri della F(s) si può dedurre l'andamento della f(t) di partenza. A tale fine si osserva che:

ad un polo singolo nell'origine è associata una funzione esponenziale

a due poli complessi coniugati sono associate funzioni di tipo sinusoidale

se i poli si trovano nel semipiano destro, oppure se esistono poli multipli sull'asse immaginario, la f(t) diverge

se i poli si trovano nel semipiano sinistro la f(t) converge

Si tenga presente che l'esponenziale tende a zero tanto più rapidamente quanto più il polo, reale e negativo, è lontano dall'origine; maggiore è, invece, la distanza dall'asse reale dei poli complessi coniugati e più elevata è la frequenza di oscillazione.