(4.5.6.1)4.5.6. - Poli complessi coniugati
(4.5.6.1)
Se i poli sono complessi coniugati 
, conviene considerare nel suo
complesso il contributo al modulo e alla fase dei due fattori 
e 
. A denominatore dell'equazione
(4.5.6.1) si ha:
Per evidenziare alcuni aspetti concettuali essenziali, si scrive il denominatore della (4.5.6.1) nel seguente modo:
(4.5.6.2)
avendo posto:
(4.5.6.3)
La costante 
che deriva da questa trasformazione viene conglobata nella costante K
della f.d.t. complessiva.
Per quanto riguarda il significato dei parametri w o e x , con riferimento alla posizione dei poli nel piano di s, il coefficiente w o, chiamato pulsazione naturale, è legato ai poli dalla relazione
(4.5.6.4)
e rappresenta la distanza dei poli dall'origine; il coefficiente x , detto coefficiente di smorzamento, è dato da
.
(4.5.6.5)
Nel caso in cui sia q = 0°, e quindi x = 1, i poli sono reali e coincidenti e lo smorzamento viene detto critico. Se invece q = 90°, lo smorzamento è nullo e i poli sono puramente immaginari.
Per valori di x maggiori di uno, i poli diventano reali e distinti e l'equazione (4.5.6.5) perde ovviamente di significato.
In caso di poli reali il tracciamento del diagramma di Bode risulta dalla somma dei diagrammi relativi ai due poli.
La f.d.t. è espressa, quindi, da
,
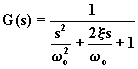(4.5.6.6)
e ponendo s = jw , si ottiene:
.
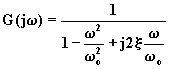(4.5.6.7)
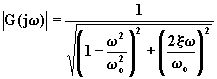(4.5.6.8)
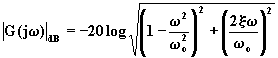(4.5.6.9)
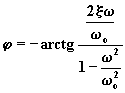(4.5.6.10)
La curva del modulo presenta due asintoti:
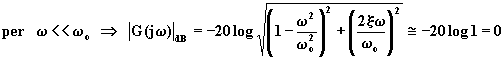
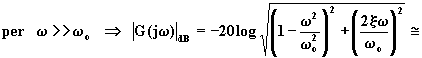
(4.5.6.12)
L'equazione (4.5.6.11) rappresenta una retta coincidente con l'asse
delle ascisse; l'equazione (4.5.6.12) rappresenta una retta decrescente di pendenza 
, che interseca l'asse
delle ascisse per 
.
Pertanto il diagramma asintotico di Bode del modulo della funzione espressa mediante
l'equazione (4.5.6.8) è costituita da due spezzate che si incontrano nel punto 
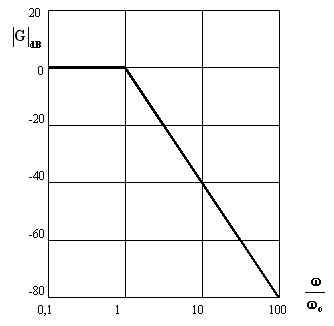
prima spezzata
seconda spezzata
dove 
è la pulsazione normalizzata
Nella maggior parte dei casi, però, la rappresentazione asintotica del modulo non fornisce un'approssimazione accettabile della curva reale il cui andamento dipende fortemente dal valore di x .
L'analisi matematica mette in evidenza l'esistenza di un massimo della curva in corrispondenza della pulsazione
(4.5.6.13)
di valore
.
(4.5.6.14)
Infatti:
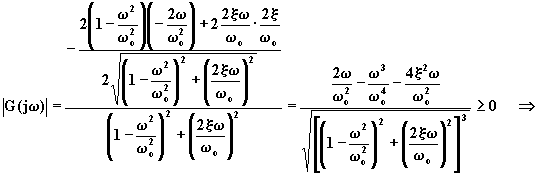
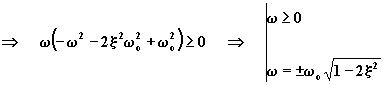
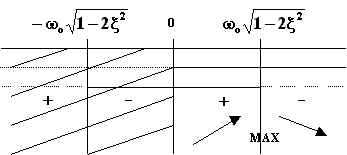
MAX per 
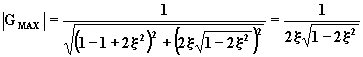
L'equazione (4.5.6.13) ha significato solo per valori reali di w , ossia per 
;
pertanto si avrà un massimo superiore a 1, cioè a 0dB, solo se 
. In condizione di smorzamento nullo (x
= 0, poli puramente immaginari) il massimo vale infinito e si verifica per 
. Da quanto detto risulta evidente la
necessità di disporre delle curve reali, ottenute per diversi valori di x .
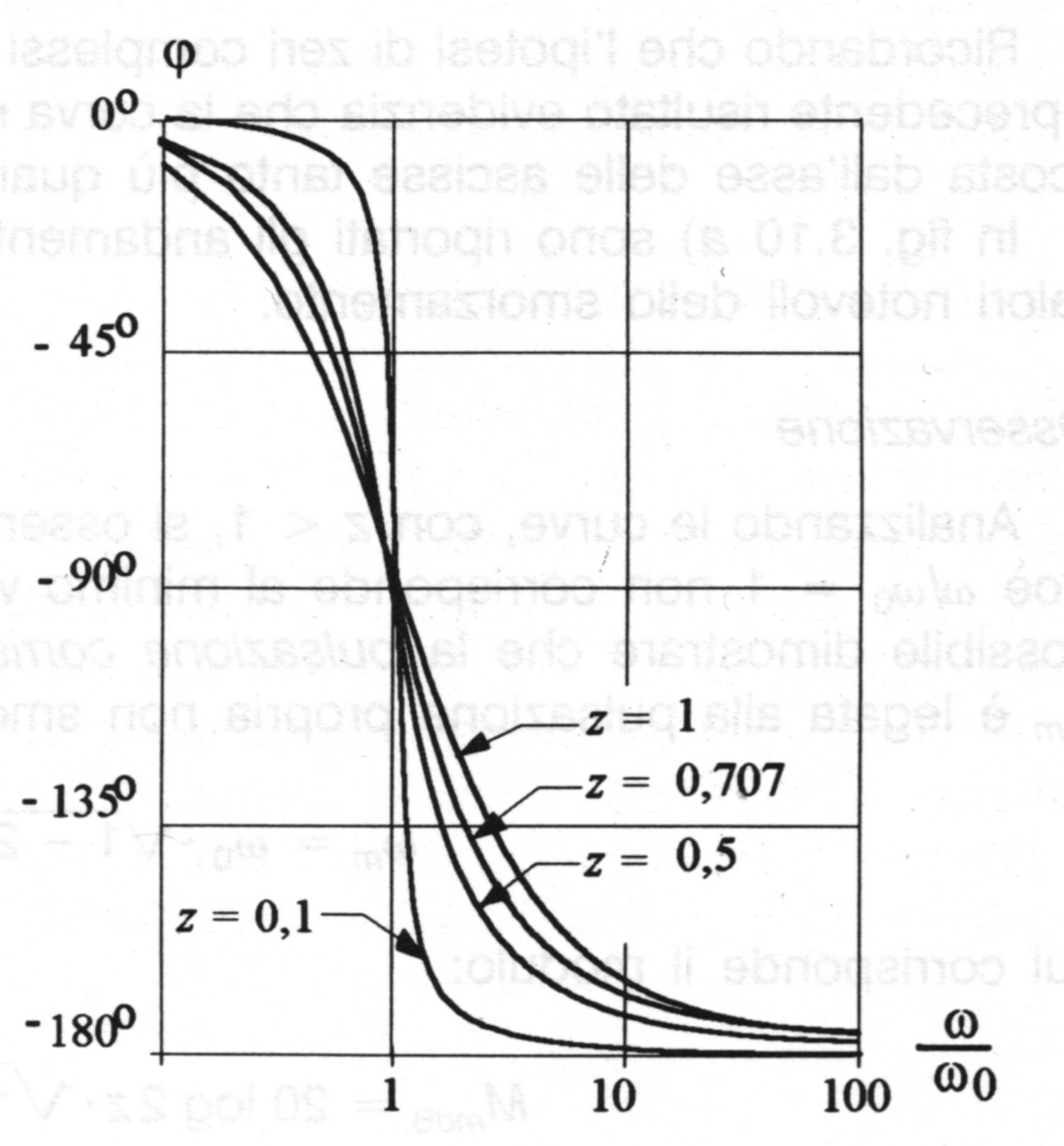
In figura sono riportate le curve in funzione della pulsazione normalizzata w /w o per alcuni valori di x .
Nel caso in cui (q = 45°), la curva assume la massima piattezza prima di decrescere
con pendenza . La
risposta è allora quella tipica di un filtro passa-basso con pulsazione di taglio 
. Infatti, per questa pulsazione dall'equazione
(4.5.6.8) si ricava: 
.
Questo tipo di risposta e la corrispondente distribuzione dei poli nel piano di s sono detti alla Butterworth.
Anche per la fase si determinano gli asintoti:
Supponendo che 
, si ha:
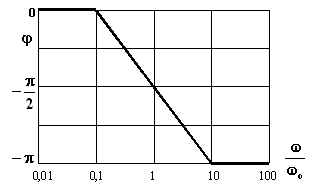
Tale rappresentazione asintotica della fase non fornisce una approssimazione accettabile della curva reale il cui andamento dipende fortemente da x . Lo scostamento si ha soprattutto per la spezzata centrale del diagramma.
A tal fine si può calcolare la pendenza della retta tangente alla
curva per per
diversi valori de x .
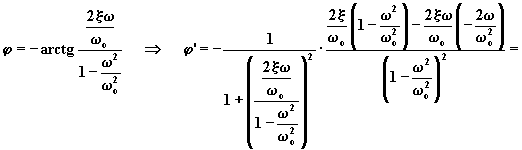
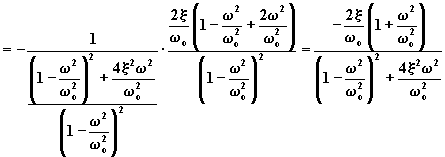
Per ,
si ha: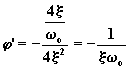 
.
La pendenza nel punto dipende anche dal valore di w o.
assumendo 
, si
calcola la pendenza nel punto per alcuni valori di x :
utilizzando tali dati si può tracciare in linea di massima l'andamento delle curve reali per i su usati valori di x .
