(4.5.7.1)4.5.7. - Zeri complessi coniugati
(4.5.7.1)
Ponendo s = jw , si ottiene:
.
(4.5.7.2)
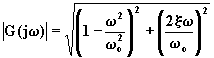(4.5.7.3)
(4.5.7.4)
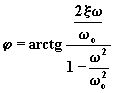(4.5.7.5)
La curva del modulo presenta due asintoti:
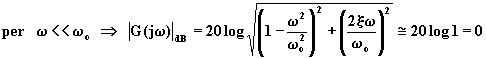
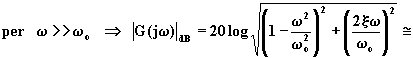
(4.5.7.7)
L'equazione (4.5.7.6) rappresenta una retta coincidente con l'asse
delle ascisse; l'equazione (4.5.7.7) rappresenta una retta crescente di pendenza 
, che interseca l'asse
delle ascisse per 
.
Pertanto il diagramma asintotico di Bode del modulo della funzione espressa mediante
l'equazione (4.5.7.3) è costituita da due spezzate che si incontrano nel punto 
L'analisi matematica mette in evidenza l'esistenza di un minimo della curva in corrispondenza della pulsazione
(4.5.7.8)
di valore
.
(4.5.7.9)
In figura sono riportate le curve in funzione della pulsazione normalizzata w /w o per alcuni valori di x .
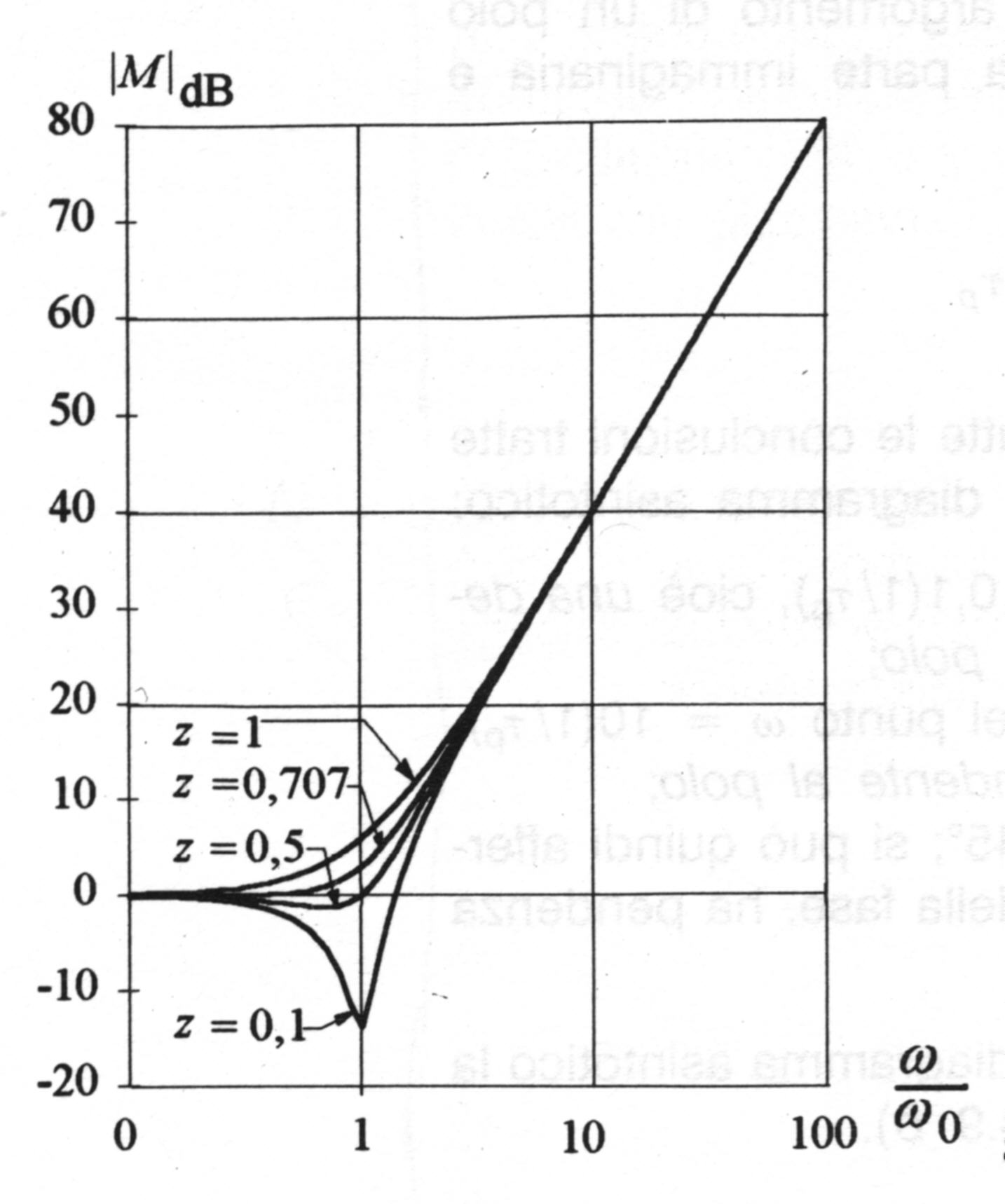
Anche per la fase si determinano gli asintoti:
L'andamento delle curve reali per alcuni valori di x
sono riportate in figura in funzione di 
.
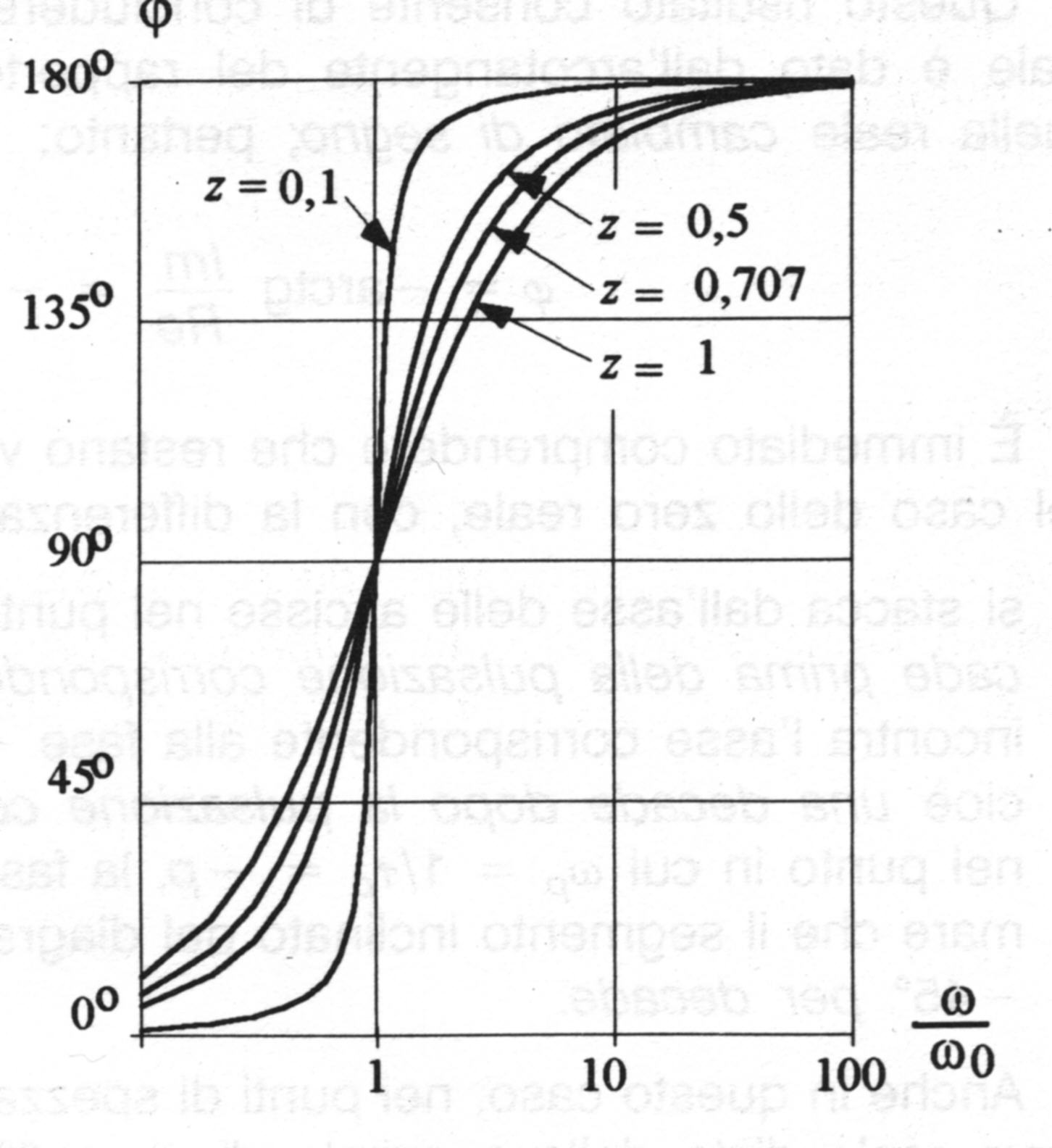
Queste considerazioni si riferiscono a zeri con parte reale negativa. Se gli zeri giacciono invece nel semipiano di destra (parte reale positiva), fermo restando quanto detto per il modulo, la fase varia da 0 a -p .
