5. - RAPPRESENTAZIONE SIMBOLICA DI GRANDEZZE SINUSOIDALI

5.1. - Vettori e numeri complessi

In un piano complesso (piano di Argante-Gauss), un vettore viene univocamente determinato dall'espressione

                   ,                      (5.1.1)                             

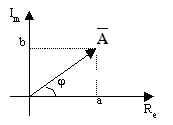
essendo a la sua componente lungo l'asse reale, ossia parte reale del vettore, jb la sua componente lungo l'asse immaginario, ossia parte immaginaria del vettore. Il vettore viene, quindi, individuato da un numero complesso. D'altronde, all'espressione si potrà fare sempre corrispondere nel piano complesso un vettore , avente per componenti a e jb. Un numero complesso può quindi essere rappresentato graficamente con un vettore il cui modulo è:

                                                                                                             ,                                                      (5.1.2)

che è anche il modulo del numero complesso, e con un angolo j , la cui tangente è:

                                                                                                                    ,                                                           (5.1.3)

che è l'argomento del numero complesso.

j è la particella immaginaria, definita dalla relazione .

Un numero complesso può, però, essere posto in forma differente da quella cosiddetta binomia . Infatti, indicati con A il modulo e con j l'argomento, le componenti a e jb possono essere poste nella seguente forma:

                                                                              ,                               (5.1.4)

per cui:

                                                                      ,                         (5.1.5)

che esprime il numero complesso in forma trigonometrica.

Inoltre, ricordando le formule di Eulero                  ,                                                   (5.1.6)

ad si potrà associare la seguente espressione:

                                                                                          ,                                             (5.1.7)

detta forma esponenziale del numero complesso.