6.13.2. - Filtro passa-alto

La f.d.t. presenta un polo reale e negativo e uno zero nell'origine:

                                                                                                                             (6.13.2.1)

avendo indicato con l'unico polo e supposto . Posto , si ha:

                                                                                                                        (6.13.2.2)

Al variare di w si deducono le seguenti relazioni:

Una rete con funzione di trasferimento di questo tipo lascia passare le alte frequenze ed attenua le basse frequenze; per questo motivo essa può essere genericamente chiamata filtro passa-alto.

Per disegnare i diagrammi di Bode si ricava il modulo e la fase della f.d.t. con , risulta:

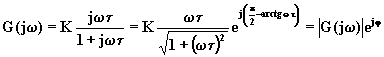                                                              (6.13.2.3)

Pertanto il modulo, espresso in forma logaritmica, e la fase j valgono:

                                                                         (6.13.2.4)

                                                                                                                                 (6.13.2.5)

Gli asintoti del modulo sono:

Il diagramma di Bode del modulo è costituito da due spezzate che si incontrano nel punto , la prima crescente con una pendenza di , la seconda parallela all'asse delle ascisse.

Gli asintoti del diagramma della fase sono:

Il diagramma della fase è costituito da tre spezzate.

Per l'ampiezza del modulo della f.d.t. risulta diminuito di rispetto al valore dell'asintoto orizzontale:

,

mentre lo sfasamento è pari a p /4. La pulsazione che determina una tale variazione del modulo della f.d.t. rispetto all'asintoto orizzontale viene chiamata pulsazione di taglio. La pulsazione di taglio coincide col valore assoluto dell'unico polo della f.d.t..

Il diagramma di Nyquist è a forma di semicerchio ed occupa il primo quadrante perché lo sfasamento è compreso tra 0 (quando il modulo è uguale a K) e p /2 (quando il modulo è uguale a zero).