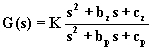6.14. - Sistemi del secondo ordine in regime sinusoidale

Si dicono del secondo ordine quei sistemi la cui funzione di trasferimento presenta due poli. Poiché il numero degli zeri non può superare il numero dei poli, una f.d.t. con due poli può avere al più due zeri. Sia gli zeri che i9 poli possono essere reali oppure complessi coniugati, inoltre, affinché la rete sia stabile, i poli devono avere parte reale negativa. La tipica f.d.t. è la seguente:

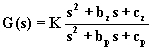                                                                           .                                                 (6.14.1)

Nell'ipotesi che i poli possano essere complessi coniugati, conviene esprimere la f.d.t. in forma normalizzata. Indicando con e le radici dell'equazione che si ottiene uguagliando a zero il polinomio a numeratore o al denominatore, risulta:

                                                      ,                          (6.14.2)

dalla quale si trae: e ,

(qualora interessi la risposta al gradino viene utilizzato il parametro 2a in sostituzione di ) che sostituiti nella (6.14.1), danno la forma normalizzata:

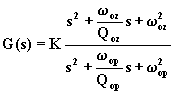                                                                            ,                                          (6.14.3)

Nell'ipotesi di radici complesse coniugate, si ha: ;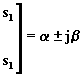

dall'equazione (6.14.2) si trae:

                                                                                                                                (6.14.4)

                                                                                                                                (6.14.5)

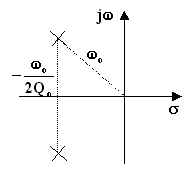
Supponendo che il polinomio in esame sia quello al denominatore, dal diagramma poli-seri e dalle equazioni (6.14.4) e (6.14.5) si deduce che l'ascissa comune a dei due poli è uguale a e che la distanza di ciascun polo dall'origine vale .

Si osservi che il parametro è ovviamente positivo; se le radici debbono avere parte reale negativa, anche il parametro risulta positivo. Ne segue che, nell'equazione (6.14.3), soltanto il termine al numeratore può risultare negativo, oltre ovviamente alla quantità costante K.

Il fatto che i poli e gli zeri risultino reali o complessi, dipende dal segno del , ossia della quantità

                                                                                .                                                       (6.14.6)

Perché la disequazione non perda di significato deve risultare in ogni caso . è una quantità sempre positiva; per si hanno poli o zeri coincidenti nell'origine. Premesso ciò, è possibile semplificare la quantità , e si ottiene:

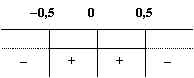
Considerando solo valori positivi di , si ha:

Dalla f.d.t. generalizzata si possono dedurre diverse funzioni di trasferimento supponendo che al numeratore compaiono uno o due termini soltanto. A ciascuna di esse corrispondono diversi diagrammi di Bode e, quindi, una diversa risposta in frequenza del circuito. Nel seguito si supporrà per semplicità che sia e .

Il parametro è talvolta detto pulsazione dell'oscillazione non smorzata.

Il parametro , detto coefficiente di qualità o fattore di merito, è legato al così detto fattore di smorzamento x :

.