6.14.2. - Poli complessi coniugati e poli reali coincidenti

Il modulo della espressa dalla (6.14.1.2) è il seguente:

                                                            ;                                    (6.14.2.1)

Da tale relazione si deduce che:

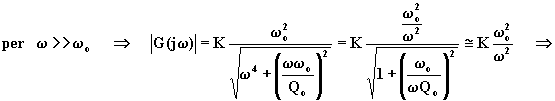
Alla prima relazione corrisponde una retta orizzontale, alla seconda una retta decrescente con pendenza . I due asintoti si incontrano nel punto , che rappresenta pertanto il punto di rottura.

Per in realtà risulta: ; all'aumentare di il diagramma di Bode per i moduli in prossimità di si incurva verso l'alto e presenta un massimo qualora risultino reali le soluzioni dell'equazione . Indicando con la soluzione di questa equazione, si può dimostrare che essa vale:

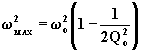                                                                                                                   (6.14.2.2)

Affinché sia reale è necessario che sia . Pertanto, all'aumentare di e per valori di compresi tra e , la curva del diagramma di Bode per il modulo si sposta verso l'alto senza avere un massimo; per la curva presenta un picco per ; tale valore è sicuramente inferiore a e tende a all'aumentare di , ossia all'accentuarsi del picco.

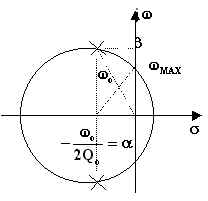
L'equazione (6.14.2.2) può essere facilmente dedotta per via geometrica dal diagramma poli-zeri. Disegnato il cerchio con centro sull'ascissa comune dei due poli e diametro pari alla distanza tra i due poli, ossia uguale alla parte immaginaria dei poli, il punto di intersezione di questo cerchio con l'ordinata positiva individua la .

Esprimendo, infatti, il raggio del cerchio sia in funzione di che di e si ottiene:

,

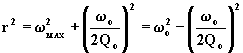risolvendo rispetto a si ha:

.

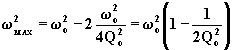Il cerchio di figura prende il nome di cerchio di picco. Tenendo conto che: e , si ha:

.

Tale relazione evidenzia che è reale, cioè esiste, se è ; pertanto ha un massimo soltanto se l'ordinata del polo è maggiore dell'ascissa. Se il cerchio di picco non interseca l'asse delle ordinate la curva di risposta non presenta alcun picco.

Quando la curva è massimamente piatta il cerchio di picco risulta tangente all'asse delle ordinate, ed i poli sono a 45°. Tale distribuzione dei poli è un caso particolare della più generale distribuzione di Butterworth, che assicura un diagramma di Bode per i moduli massimamente piatto con un numero qualsiasi di poli purché uniformemente distribuiti, assieme ai poli speculari rispetto all'asse delle ordinate in un cerchio con centro nell'origine e passante per i poli.

La fase della (6.14.1.2), supposto , risulta:

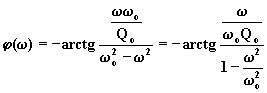                                                                                      (6.14.2.3)

Anche la fase dipende dal valore di .