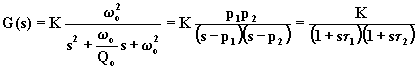6.14.3. - Poli reali e distinti

Qualora i poli siano reali e distinti non conviene usare la forma normalizzata della f.d.t.. Indicando con p₁ e p₂ i due poli, si ha:

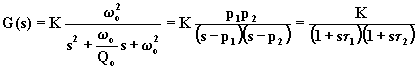                                                    (6.14.3.1)

avendo posto e . Qualora sia i due poli sono coincidenti.

Posto , si può ricavare il modulo della f.d.t.:

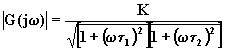
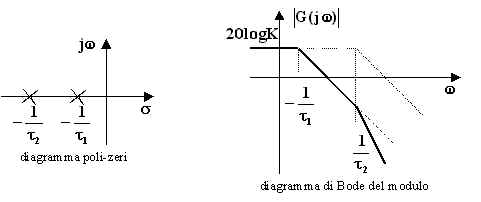
Il diagramma complessivo di Bode per i moduli si ricava sommando tra loro due diagrammi del tipo definito dalla (6.13.1.4), uno con punto di rottura e l'altro . Si osservi che la pendenza del primo asintoto è uguale a e quella del secondo ; per si ritrova pertanto il risultato già ottenuto nel caso di poli reali e coincidenti.

Indicando con j la fase di si può scrivere:

.

Anche il diagramma asintotico di Bode per la fase si ottiene sommando tra loro due diagrammi del tipo definito dall'equazione (6.13.1.5); pertanto la fase complessiva può variare da 0 a -180°.

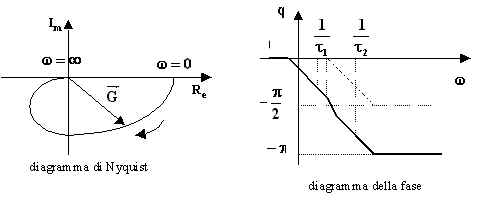
Il diagramma di Nyquist occupa il terzo e il quarto quadrante perché lo sfasamento è compreso tra 0 e -180°.