6.7. - Risposta di una rete nel dominio del tempo

La funzione di rete H(s) è un numero complesso e può, quindi, essere rappresentata in forma esponenziale. Posto , risulta:

                                                                                                                              (6.7.1)

dove rappresenta il modulo di e j l'argomento, ambedue funzioni di w . Si osservi che e sono grandezze caratteristiche di una rete: rappresenta il rapporto tra le ampiezze della risposta e dell'eccitazione, lo sfasamento.

Scegliendo opportunamente l'inizio dell'asse dei tempi, un'eccitazione x(t) di tipo sinusoidale può essere così espressa:

                                                                                                                                   (6.7.2)

pertanto la risposta y(t) a tale eccitazione di un circuito in regime sinusoidale risulta in generale:

                                                                         ,                                                (6.7.3)

dove Y_M e j sono quantità che debbono essere determinate.

Associando a x(t) e y(t) i relativi fasori e e risolvendo il circuito col metodo simbolico, si ottiene:

                                                                                                                          (6.7.4)

segue:                        .

Nota la funzione di rete del circuito e il segnale d'ingresso risulta pertanto definita anche la risposta nel dominio del tempo.

Raccogliendo w nell'equazione (6.7.3), si ottiene:

                                                                       ,                                            (6.7.5)

dove j /w ha le dimensioni di un tempo. Dalle espressioni nel dominio del tempo dell'eccitazione e della risposta che non solo esse hanno ampiezze diverse, ma traslano tra loro rispetto al tempo.

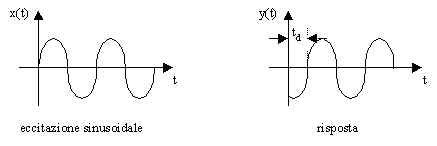
Ad esempio, ad uno sfasamento negativo corrisponde un ritardo nel tempo pari a j /w :

                                                                                      .                                                        (6.7.6)

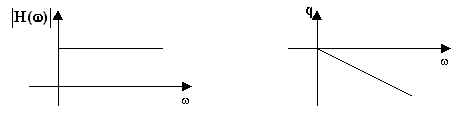
Affinché l'ampiezza del segnale d'uscita e il ritardo t_d non dipendano dalla pulsazione ), occorre che si abbia ; in tale caso le curve caratteristiche (ossia gli andamenti di in funzione di w ) sono quelle di figura.

Il tempo t_d espresso dall'equazione (6.7.6) viene chiamato ritardo di fase e si può così scrivere:

                                                                                 .                                                   (6.7.7)

Pertanto, se la rete introduce uno sfasamento fra eccitazione e risposta al più di p /2, il ritardo di fase al più può essere pari a T/4. Più in generale, se è , segue .