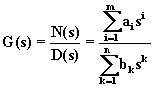6.8. - Funzione di trasferimento generalizzata

Nel dominio della frequenza le equazioni di una rete in regime sinusoidale sono di tipo algebrico. La funzione di rete, oppure quella di trasferimento, risultano pertanto espresse come rapporto tra due polinomi nella variabile s, i cui coefficienti sono reali e costanti perché tali si suppongono i parametri R, L e C della rete; segue:

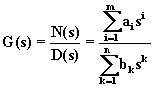                                                                                                     .                                        (6.8.1)

Un polinomio può essere decomposto in fattori, nel seguente modo:

,

dove sono le radici (cioè le soluzioni) dell'equazione che si ottiene uguagliando a zero il polinomio ed il simbolo , chiamato produttoria, indica il prodotto di n termini del tipo con i variabile da 1 a n. Poiché i coefficienti sono, per ipotesi, reali, le radici dell'equazione algebrica sono reali, oppure complesse coniugate. Per determinare tali radici è necessario supporre che la variabile s sia complessa, ossia scrivere . Una funzione di trasferimento nella quale vengono indicate esplicitamente le radici dei polinomi al numeratore e al denominatore prende il nome di funzione di trasferimento generalizzata.